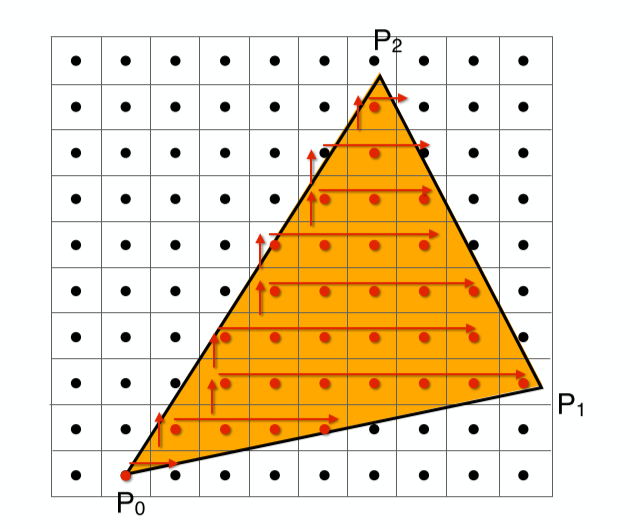
标准立方体到屏幕
什么是屏幕?
- 二维数组
- 每个元素是一个像素
- 一种经典的光栅成像设备
Raster在德语中的意思就是表示屏幕
光栅化:在屏幕上绘画
像素:
- 在屏幕上最小单位的小方块
- 由红绿蓝三原色混合而成
屏幕空间
- 像素都是以 (x,y) 的形式表示,其中 x, y 都是整数
- 像素的范围从 (0, 0) 到 (宽度 – 1, 长度 – 1)
- 像素的中心在 (x + 0.5, y + 0.5)
- 屏幕覆盖范围为 (0, 0) 到 (宽, 高)
视口变换
- Z 轴被忽略
-
将原本 [-1,1]^2 的正方体变换为 [0, 宽] \times [0, 高](视口变换)
-
视口变换矩阵
M_{viewport}=\begin{pmatrix}
\dfrac{width}{2} &0 &0 &\dfrac{width}{2} \\
0 &\dfrac{height}{2} &0 &\dfrac{height}{2} \\
0 &0 &1 &0 \\
0 &0 &0 &1
\end{pmatrix}
光栅显示设备
-
阴极射线管
- 隔行扫描:但是出现的问题是高速运动的画面会构成画面撕裂
-
CRT显示器
-
示波器
-
帧缓冲器
-
平板显示设备
- LCD(液晶显示器)
- 利用液晶原理来控制一个像素显示什么
- 液晶通过自己的不同排布影响光的极化
- OLED
- LED(发光二极管)
- 电子墨水屏:控制黑的在上还是白的在上。但是缺陷是刷新率肉眼可见的慢
- LCD(液晶显示器)
三角形-基本形状单元
- 最基础的多边形
- 任何多边形都可以拆成三角形
- 独特的性质
- 除非折成两个三角形,否则永远是一个面
- 三角形的内外很明确
- 可以利用重心插值进行三角形顶点插值
光栅化中最重要的一步:判断三角形与一个像素(中心点)的位置关系
采样
定义:一个函数离散化的过程
for (int x = 0; x < xmax; ++x) output[x] = f(x);
采样可以是一维,二维,三维的。光栅化属于二维采样
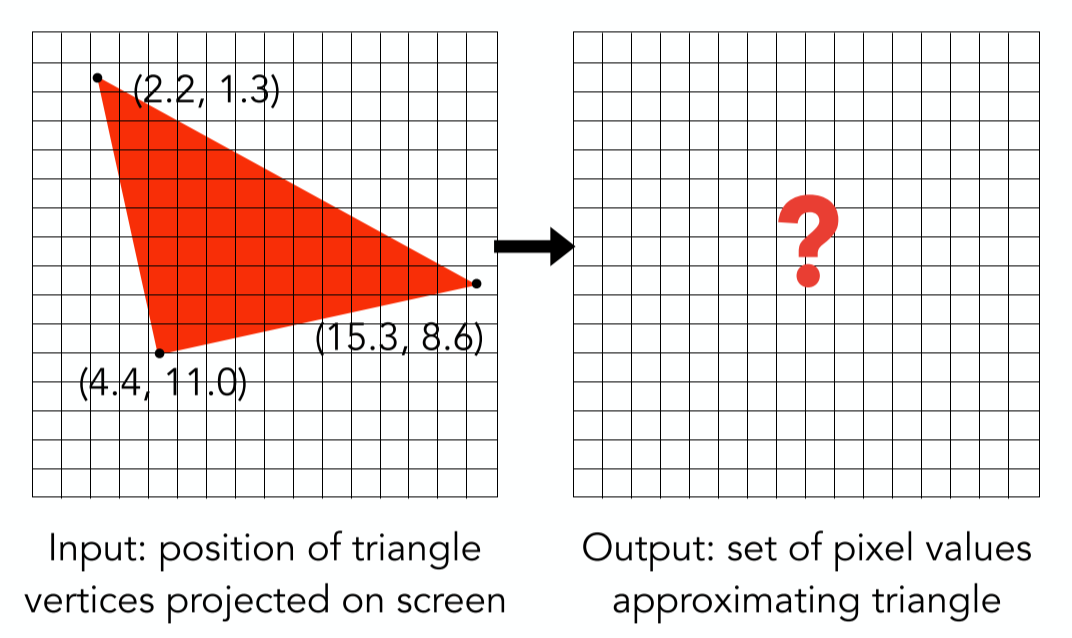
光栅化的方法
给一个三角形,来判断像素中心是否在三角形内
定义一个二元函数 inside(tri, x, y)
\text{inside(t, x, y)}
\begin{cases}
1 &\text{ Point (x,y) in triangle t }\\
0 &\text{ otherwise }
\end{cases}
光栅化 = 对 2D 指标函数进行采样
for (int x = 0; x < xmax; ++x)
fot (int y = 0; y < ymax; ++y)
image[x][y] = inside(tri, x + 0.5, y + 0.5);
遍历所有点,判断所有点是否在像素内,通过叉乘计算出(见叉乘在图形学的应用)点是否在三角形内。
点在三角形边上怎么处理:看自己定义(在边上不算,或者都算)
API(OpenGL)的严格规定:落在三角形的边的左边和上边就算,其次不算
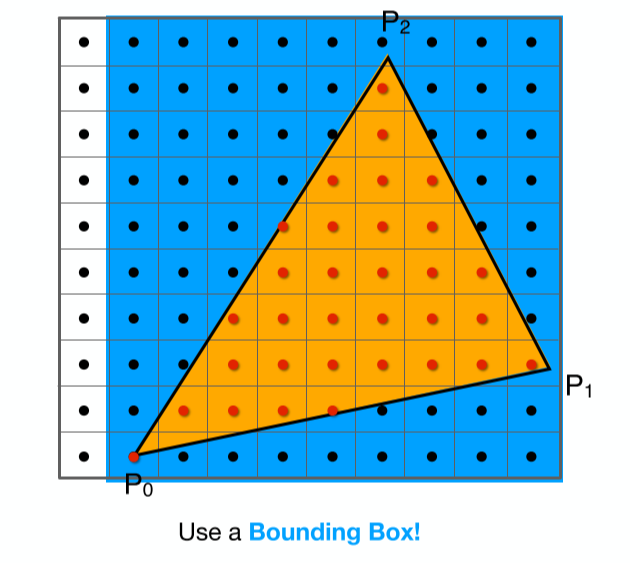
快速寻找像素:
- 蓝色区域表示三角形的包围盒,只有在这个区域内的像素,才去做上面的
for循环;即不需要每一个像素都从(0 - width / height)走一遍 -
AABB 法
- 三角形所覆盖的区域,每一行都找最左和左右,这样就不考虑多一个像素,但是方法较难
- 三角形窄长,又是旋转了角度的,AABB 的方法就比较合适