MVP 矩阵

什么是MVP矩阵？

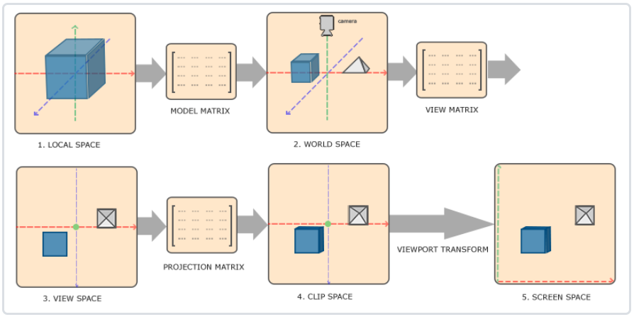
MVP矩阵分别是模型（Model），观察（View），投影（Projection）三个矩阵。我们的顶点坐标起始于局部空间（Local Space），在这里它称为局部坐标（Local Coordinate），它在之后会变为世界坐标（World Coordinate），观察坐标（View Coordinate），裁剪坐标（Clip Coordinate），并最后以屏幕坐标（Screen Coordinate）的形式结束

M矩阵：模型空间 → 世界空间的转换矩阵

模型空间是以自身中心为原点的空间坐标系

世界空间是以世界中心为原点的空间坐标系

在不同的建模软件或者游戏引擎中使用的坐标系是不一样的，比如OpenGL使用的的右手坐标系，DirectX 使用的是左手坐标系

两种坐标系怎么区分呢？正 x 轴指向右面，正 y 轴指向上面。通过沿正 x 轴方向到正 y 轴方向握拳，大拇指的指向就是相应坐标系统的正 z 轴的指向。在握拳的过程中，如果是顺时针方向就是左手坐标系，如果是逆时针方向就是右手坐标系。在 Unity 中使用的是左手坐标系

从模型空间变换到世界空间：

1. 第一步进行了缩放

2. 第二步进行了旋转

3. 第三步进行了平移

$$P_{new}=M_{translation}M _{rotation}M_{scal}P_{old}$$

一个三维场景中的各个模型一般需要各自建模，再通过坐标变换放到一个统一的世界空间的指定位置上，这个过程再3D图形学称作 “世界变换”，实际变换有三种，平移、旋转和缩放（实际上还有不常用的的扭曲和镜像，他们不是仿射变换），这三种变换按各种顺序执行，结果是不同的。可是实际的应用中一 般按照 缩放 → 旋转 → 平移的顺序进行。这样做的原因是可以获得最符合常理的变换结果。

比方说，通过世界变换希望获得的结果可能是：将一个放在原点的物体（比如说可乐罐）移动到（30，50），让它自身倾斜 45° ，再放大 2 倍

而不希望的结果是：和本地坐标轴成角度的缩放（会导致扭曲，像踩扁的可乐罐）绕自己几何中心以外位置的原点的旋转（地球公转式）和缩放

而颠倒了上述变换顺序就会得到这样不自然的结果。具体地说：当缩放在旋转之后进行时，会发生现象一。当缩放和旋转在平移之后进行时会发生现象二。

这时因为：在物体刚刚放入世界坐标系的时候使用的是本地坐标，也就是本地和全局坐标系的原点和坐标轴都是重合的（当然两者分别使用了左右手坐标系除外，那是BUG），此时所有物体都“把世界坐标系当做自己的本地坐标系”

而经过坐标变换后：

缩放变换不改变坐标轴的走向，也不改变原点的位置，所以两个坐标系仍然重合

旋转变换改变坐标轴的走向，但不改变原点的位置，所以两个坐标系坐标轴不再处于相同走向

平移变换不改变坐标轴走向，但改变原点位置，两个坐标系原点不再重合

所以我们需要先进行缩放，再旋转，在平移，如上节所说的那样，完全可以将缩放矩阵，旋转矩阵，平移矩阵进行矩阵乘法计算，获得最后的复合变换矩阵 P_{new}=M_{CompositeTransform}P_{old} ，这样计算也不会影响最终结果。

顶点坐标从模型坐标变换到世界坐标
M_{CompositeTransform}=\begin{bmatrix}1&0&0&t_x\\0&1&0&t_y\\0&0&1&t_z\\0&0&0&1\end{bmatrix}_{translation}\begin{bmatrix}\cos\theta&-\sin\theta&0&0\\\sin\theta&\cos\theta&0&0\\0&0&0&0\\0&0&0&1\end{bmatrix}_{rotation}\begin{bmatrix}x&0&0&0\\0&y&0&0\\0&0&z&1\\0&0&0&1\end{bmatrix}_{scale}

V 矩阵：世界空间 → 视觉空间的转换矩阵

视觉空间是以摄像机中心为原点的空间坐标系，在视觉空间中使用的是右手坐标系

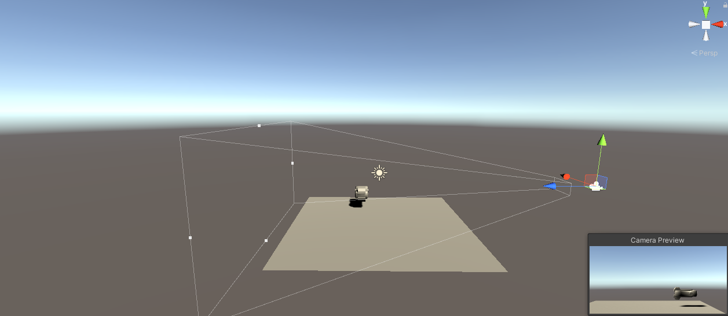
平移整个观察空间，摄像机原点和世界坐标原点重合，坐标轴重合，也就是将观察空间坐标系平移到世界空间坐标系，让两个空间坐标系重合，就可以求出这个 View 变换矩阵

因为摄像机是在世界空间中是先旋转，再平移，为了让摄像机与世界坐标重合，所以我们需要逆变换

如何进行逆变换？

先进行平移，再进行旋转，最后对 Z 分量取反（因为世界空间坐标系是左手坐标系，而视觉空间的坐标系是右手坐标系，所以我们需要对 Z 分量进行取反），即
V_{view}=\begin{bmatrix}1&0&0&0\\0&\cos\theta&-\sin\theta&0\\0&\sin\theta&\cos\theta&0\\0&0&0&1\end{bmatrix}\begin{bmatrix}1&0&0&t_x\\0&1&0&t_y\\0&0&1&t_z\\0&0&0&1\end{bmatrix}

P矩阵：视觉空间 → 裁剪空间

1. 不是真正的投影,为投影做准备。

2. 目的：判断顶点是否在可见范围内。

3. P矩阵：对 x,y,z 分量进行缩放，用 w 分量做范围值。如果 x,y,z 都在 w 范围内，那么该点在裁剪空间内。

透视投影

透视投影是符合我们人眼视觉的投影，即近大远小

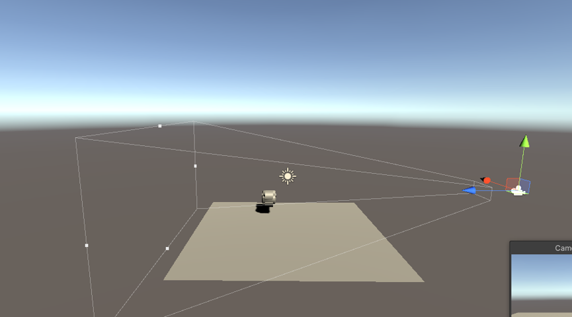
透视矩阵推导

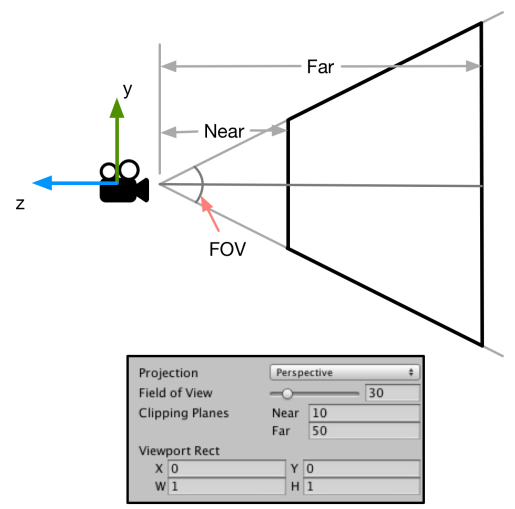
由图像可知，在 Camera 组件中，可以通过 Field of View（简称 FOV）属性来改变视锥体竖直方向的张开角度，而 Clipping Planes 中的 Near 和 Far 参数可以控制视锥体的近裁剪平面和原裁剪平面距离摄像机的远近。这样我们可以求出视锥体近裁剪平面和原裁剪平面的高度，也就是
\text{nearClipPlaneHeight}=2\cdot Near\cdot\tan\dfrac{FOV}{2}\\
\text{farClipPlaneHeight}=2\cdot Far\cdot\tan\dfrac{FOV}{2}
利用三角函数得到，前面也说 Fov 是视锥体竖直方向的张开角度，想要求出视锥体近裁剪平面的高度 Near 为已知，且是三角形的其中一个直角边，三角形直角边对边比邻边是 \tan ，原公式为
\dfrac{\dfrac{\text{nearClipPlaneHeight}}{2}}{Near}=\tan\dfrac{Fov}{2}
而这仅仅是近裁剪平面的一半，所以我们需要乘 2。

即
\dfrac{\text{nearClipPlaneHeight}}{2\cdot Near}=\tan\dfrac{Fov}{2}
通过移项，得到最后的公式
\text{nearClipPlaneHeight}=2\cdot Near\cdot \tan\dfrac{Fov}{2}
这也同样适用在原裁剪平面高度，以相同的方法获得最终的原裁剪平面高度。

就这样，我们可以求出视锥体近裁剪平面和原裁剪平面的高度

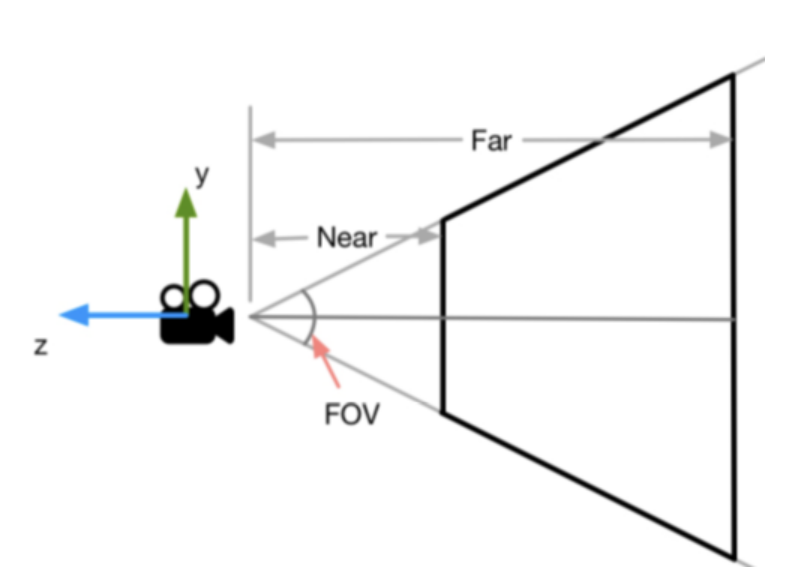
但是到现在我们还缺乏横向的信息。这也可以通过摄像机的横纵比得到。在 Unity 中，一个是摄相机的横纵比由 Game 试图的横纵比和 Viewport Rect 的 W 和 H 属性共同决定，假设，当前摄像机的横纵比为 Aspect，可以得到定义的公式
Aspect=\dfrac{\text{nearClipPlaneWidth}}{\text{nearClipPlaneHeight}}\\
Aspect=\dfrac{\text{farClipPlaneWidth}}{\text{farClipPlaneHeight}}
摄相机的横纵比由 Game 视图的横纵比和 Viewport Rect 的 W 和 H 属性共同决定，所以可知 \dfrac{W}{H}=Aspect

我们得到近裁剪平面等式关系，联立方程得
\left\{\begin{matrix}\dfrac{\text{nearClipPlaneWidth}}{\text{nearClipPlaneHeight}}=Aspect\\\dfrac{W}{H}=Aspect\end{matrix}\right.
最终得到关系式
W=\text{nearClipPlaneWidth}\newline
H=\text{nearClipPlaneHeight}
前面我们又得到 \text{nearClipPlaneHeight} 方程，所以方程联立得到

\left\{\begin{matrix}H=\text{nearClipPlaneHeight}\\2\cdot Near\cdot \tan\dfrac{Fov}{2}=\text{nearClipPlaneHeight}\end{matrix}\right.

最后得到 H 与 2\cdot Near\cdot \tan\dfrac{Fov}{2} 之间的等式关系，即
H=2\cdot Near\cdot \tan\dfrac{Fov}{2}
同理，可得
W=2\cdot Aspect \cdot Near\cdot \tan\dfrac{Fov}{2}
我们来画一张图

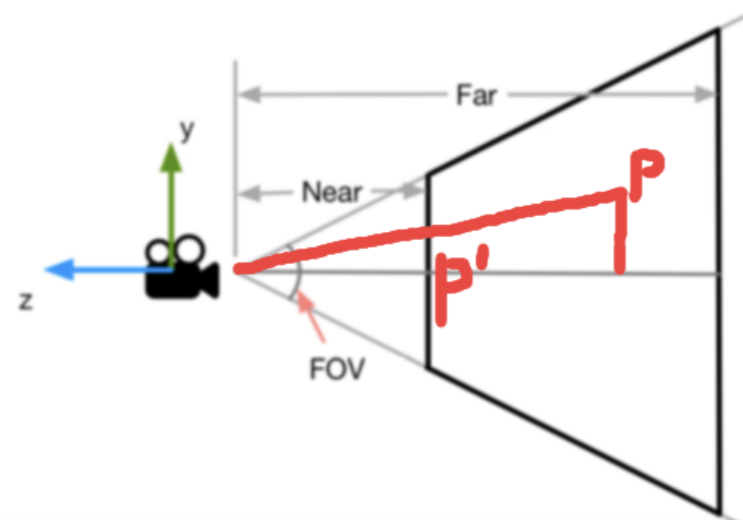
在这张图中有两点，P 与 P’ ，假设 P 坐标是 (x,y,z)，那么求的近裁剪平面的 P’ 坐标是 (x’,y’,z’)，那么问题来了，P’ 怎么求呢。？

如图，我们知道这是一个相似三角形。对于相似三角形我们有定律
\dfrac{x}{x’}=\dfrac{y}{y’}=\dfrac{z}{z’}
P’ 的 z’ 我们已知，因此可得方程

\left\{\begin{matrix}x’=x\cdot \dfrac{Near}{z}\qquad x’\in{-\dfrac{W}{2},\dfrac{W}{2}}\\y’=y\cdot \dfrac{Near}{z}\qquad x’\in{-\dfrac{H}{2},\dfrac{H}{2}}\end{matrix}\right.

我们把范围定义在 [-1,1] 之间，由于 x’,y’ 关于原点对称，所以只要分别除以 \dfrac{W}{2},\dfrac{H}{2} 转换到 [-1,1] 空间计算即可。

可得

\left\{\begin{matrix}x”=\dfrac{2x\cdot Near}{z\cdot W}\\y”=\dfrac{xy \cdot Near}{z\cdot H}\end{matrix}\right.

我们带入 W 和 H 的公式，最后得到方程组
\left\{\begin{matrix}x”=\dfrac{2x\cdot Near}{z\cdot 2\cdot Aspect \cdot Near\cdot \tan\dfrac{Fov}{2}}\\y”=\dfrac{xy \cdot Near}{z\cdot 2\cdot Aspect \cdot Near\cdot \tan\dfrac{Fov}{2}}\end{matrix}\right.

化简得

\left\{\begin{matrix}x”=\dfrac{x}{z\cdot Aspect\cdot \tan\dfrac{Fov}{2}}\\y”=\dfrac{y}{z\cdot \tan\dfrac{Fov}{2}}\end{matrix}\right.

有的人可能会在不同的资料书上看到的公式是这样
\left\{\begin{matrix}x”=\dfrac{x\cot\dfrac{Fov}{2} }{z\cdot Aspect}\\y”=\dfrac{y\cdot \cot\dfrac{Fov}{2}}{z}\end{matrix}\right.
没关系，这是正确的，只是表达方式不一样，但是所要表达的内容是完全一样的。

\cot 余切函数，在现在的三角形函数知识中，余切函数就不怎么讲了，在这里补充一下

\cot 和 \tan 的关系：\tan\theta \cdot \cot\theta = 1。在三角函数中，\cot\theta = \dfrac{\cos\theta}{\sin\theta}，当\theta\not= k\Pi，k\in Z时，\cot\theta =\dfrac{1}{\tan\theta}，当 \theta = k\Pi，k\in Z 时，\cot\theta不存在
\cot\dfrac{FOV}{2}=\dfrac{1}{\tan\dfrac{FOV}{2}}

假设 z” \in [-1,1]

所以最后得到的 p” 的坐标为 (\dfrac{x\cdot\cot\dfrac{FOV}{2}}{z\cdot Aspect},\dfrac{y\cdot\cot\dfrac{FOV}{2}}{z},z”)，至此变换后的坐标我们求出了，接下来开始求透视投影转换矩阵。

我们已知 原点 P 的坐标为 (x,y,z)，因为要进行矩阵转换，所以我们需要进行齐次坐标处理，将原点 P 提升一个维度增加 w 轴，即最后 P 点坐标是 (x,y,z,1)。

这里我们为什么要把 w 取 1。

因为要使线性变换的结果的 x 分量和 y 分量 z 分量，分别偏移 tx,ty 和 tz ，只有令w=1，才能得到正确的结果。

所以开始计算投影矩阵….但在那之前，先来回顾一下，4*4 矩阵与 4*1 矩阵计算我们最后得到什么矩阵？

没错，我们会得到 4*1 矩阵，因此得到
\begin{bmatrix}
m_{00} &m_{01}&m_{02}&m_{03}\\
m_{10} &m_{11}& m_{12}& m_{13}\\
m_{20} &m_{21}&m_{22}&m_{23}\\
m_{30}&m_{31}&m_{32} &m_{33}
\end{bmatrix}
\begin{bmatrix}
x\\
y \\
z \\
1
\end{bmatrix}=
\begin{bmatrix}
\dfrac{x\cdot\cot\dfrac{FOV}{2}}{z\cdot Aspect}\\
\dfrac{y\cdot\cot\dfrac{FOV}{2}}{z} \\
z^n \\
1
\end{bmatrix}
然后我们得到方程

m_{00}x+m_{01}y+m_{02}z+m_{03}=\dfrac{x\cot\dfrac{FOV}{2}}{z\cdot Aspect}

那么问题来了，左边的 m_{00} 和 m_{02} 如何赋值？

很简单，只需要我们把右边的向量矩阵乘个 z 就很简单了，即
\begin{bmatrix}
m_{00} &m_{01}&m_{02}&m_{03}\\
m_{10} &m_{11}& m_{12}& m_{13}\\
m_{20} &m_{21}&m_{22}&m_{23}\\
m_{30}&m_{31}&m_{32} &m_{33}
\end{bmatrix}
\begin{bmatrix}
x\\
y \\
z \\
1
\end{bmatrix}=
\begin{bmatrix}
\dfrac{x\cdot\cot\dfrac{FOV}{2}}{Aspect}\\
y\cdot\cot\dfrac{FOV}{2} \\
z^{n+1} \\
z
\end{bmatrix}
最终我们解方程得到
\begin{bmatrix}
\dfrac{\cot\dfrac{FOV}{2}}{Aspect} &0&0&0\\
0 &\cot\dfrac{FOV}{2}&0&0\\
0 &0&m_{22}&m_{33}\\
0 &0&1&0
\end{bmatrix}
然后得到
m_{22}\cdot z +m_{23}=z^{n+1}
当 z = Near 时，z” = -1，当 z = Far 时， z” = 1。

z” 的值怎么来的？

我们假设了 z”∈[-1,1] 当 z 取 Near 的时候，z” 是最小值即为-1，当 z 取 Far 的时候，z” 是最大值即为 1

所以联立方程组
\left\{\begin{matrix}
m_{22}+\dfrac{m_{23}}{Near}=-1\\
m_{22}+\dfrac{m_{23}}{Far}=1
\end{matrix}\right.
最后得到 m_{22} 与 m_{23} 的值为
\left\{\begin{matrix}
m_{22}=-\dfrac{Far-Near}{Near-Far}\\
m_{23}=\dfrac{2\cdot Near \cdot Far}{Near- Far}
\end{matrix}\right.
到此透视矩阵推导完成，最后的结果为
P_{frustTurn}=\begin{bmatrix}
\dfrac{\cot\dfrac{FOV}{2}}{Aspect} &0&0&0\\
0 &\cot\dfrac{FOV}{2} &0&0\\
0 &0&-\dfrac{Far-Near}{Near-Far}&\dfrac{2\cdot Near \cdot Far}{Near-Far} \\
0 &0 &1 &0
\end{bmatrix}

这是对于 OpenGL 的透视矩阵结果，因为OpenGL要求 w 的取值范围是 [-w，w]，但是对于 DirectX 这种图形接口，还需要对以上透视矩阵进行额外的处理，因为在 DirectX 窗口中要求的 w 的取值范围是 [0,w]，这边不再讨论。

正交投影

被投影的的物体没有远近之分，即正交视图

模型空间，世界空间，观察空间的区别

模型空间

模型空间是和某个模型或者说是对象有关的。有时模型空间也被称为对象空间或局部空间。每个模型都有自己独立的坐标空间，当它移动或旋转的时候，模型空间也会跟着它移动和旋转。比如自己的游戏模型，我们移动的时候我们的模型空间也在跟着移动，我们转身时本身的前后左右方向也跟着改变。

世界空间

世界空间是一个特殊的坐标系，因为它建立了我们所关心的最大的空间。世界空间可以被用于描述绝对位置（这里指的是世界坐标系中的位置），通常我们把世界空间的原点放置在游戏空间的中心。

在 Unity 中，除了观察空间（摄像机空间），所有的空间坐标系都是使用的左手坐标系。很多的效果都是要在世界空间中完成的，比如说我们想要让一个物体有凹凸感觉。简单而言我们想要让一个物体表面生成凹凸的感觉，我们可以使用两种贴图，一种法线贴图，一种高度图进行空间转换，在世界空间中与物体的原贴图进行混合

观察空间（摄像机空间）

最大的区别在于在观察空间中我们使用的是右手坐标系，而这个是符合OpenGL的，在观察空间中我们需要把世界空间的顶点转换到观察空间，为此我们需要求的观察空间的变换矩阵，因为坐标系的不同，所以我们需要对z轴取反，并求得逆变换，

在观察空间还有一项就是需要将观察空间的顶点转换到裁剪空间（也被称为齐次裁剪空间），这个用于变换的矩阵叫做裁剪矩阵，也被称为投影矩阵，在观察空间中并不是真正的投影，而是准备投影的数据，即那些顶点需要保留，那些需要剔除，这是由投影方式决定的