关系数据库概述
相关名词
- 关系:在关系数据库中,实体以及实体间的联系都是用关系来表示的。类似于程序设计语言中变量的概念。
- 关系模式:是对关系的描述。类似于程序设计语言中类型定义的概念。
- 关系模型:是由若干个关系模式组成的集合。
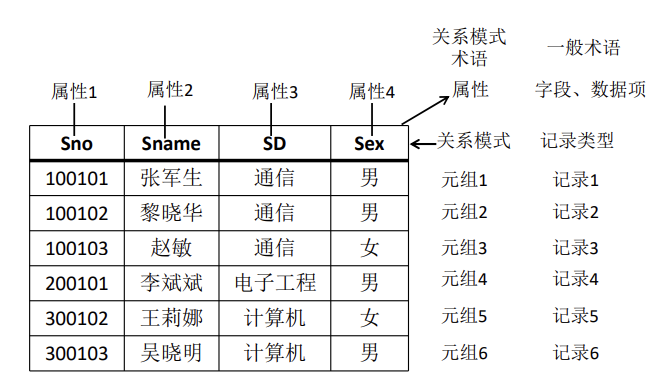
- 属性:用来描述某一个事物的特征。
- 域:每个属性的取值范围所对应一个值的集合。
- 候选码:若关系中的某一属性或属性组的值能唯一标识一个元组,则称该属性或属性组为候选码。
- 主码:又称为主键,若一个关系有多个候选码,则选定其中一个为主码。
- 主属性:包含在任何候选码中的各个属性称为主属性。
- 非主属性:不包含在任何候选码中的属性称为非主属性。
- 外码:如果关系模式 R 中的属性或属性组非该关系的码,但它是其他关系的码,那么该属性集对关系模式 R 而言是外码。
- 全码:关系模型的所有属性组是这个关系模式的候选码,称为全码。
- 元组/记录:行
- 字段、数据项
- 元数:属性的个数(列数)
- 基数:记录的个数(行数)
- $n$ 元关系:元数为几,就是几元关系。
例:关系模式:\text{Student(Sno,\ Sname,\ SD, \ Sex)}
关系数据库模式
关系模式可以表示为:\text{R(U,\ D,\ dom,\ F))}
R 表示关系名,U 是组成该关系的属性名集合;D 是属性的域;\text{dom} 是属性向域的映像集合;F 为属性间数据的依赖关系集合。
通常将关系模式简记为:R(U) 或 \text{R}(A_1\ ,A_2,\ A_3,…,\ A_n)
其中,R 为关系名,A_1,A_2,A_3,…,A_n 为属性名或域名。
例:学生关系 S 有学号 \text{Sno}、学生姓名 \text{Sname}、系名 \text{SD}、年龄 \text{SA} 属性;课程关系 C 有课程号 \text{Cno}、课程名 \text{Cname}、先修课程号 \text{PCno} 属性;学生选课关系 \text{SC} 有学号 Sno、课程号 \text{Cno}、成绩 \text{Grade} 属性。定义关系模式及主码如下(未考虑 F,即属性间的依赖关系)。
- 学生关系模式 \text{S(Sno,Sname,SD,SA)}
- 课程关系模式 \text{C(Cno,Cname,PCno),Dom(PCno)=Cno}
- 学生选课关系模式 \text{SC(Sno,Cno,Grade)}
关系的三种类型
- 基本关系(基本表或基表):它是实际存在的表,是实际存储数据的逻辑表示。
- 查询表。查询结果对应的表。
- 视图表。它是一种虚拟表,是由基本表或其他视图表导出的表。它本身是不独立存储在数据库的,数据库只存放它的定义。
关系的完整性约束
关系的完整性约束:是对关系的某种约束条件,用来保证用户对数据库作出修改时不会破坏数据的一致性,防止对数据的意外破坏。
- 实体完整性:是指基本关系R的主属性不能取空值。
-
参照完整性:
S(\underline{学号},姓名,所属院系,年龄)
D(\underline{院系编号},学院名称,学院地址,系主任)
- 用户定义完整性:是针对某一具体的关系数据库的约束条件,反映某一具体应用所涉及到的数据必须满足的语义要求。
关系运算
基本的关系代数运算
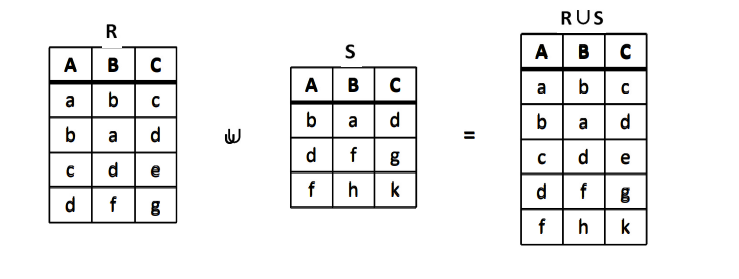
并(Union)
关系 R 与 S 具有相同的关系模式,即 R 与 S 的元数相同(结构相同),关系 R 与 S “并”由属于 R 或属于 S 的元组构成的集合组成,记作 R∪S,其形式定义如下:
R∪S=\{t|t\in R \lor t\in S\}
式中 t 为元组变量
差
关系 R 与 S 具有相同的关系模式,关系 R 与 S 的差是由属于 R 但不属于 S 的元组构成的集合,记作 R-S,其形式定义如下:
R-S=\{t|t\in R\land t\notin S\}

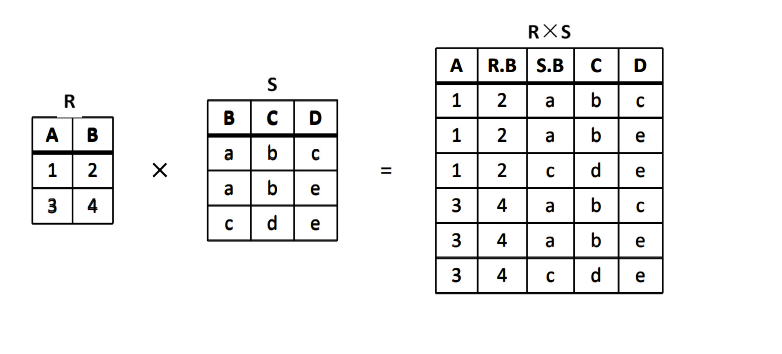
广义笛卡儿积
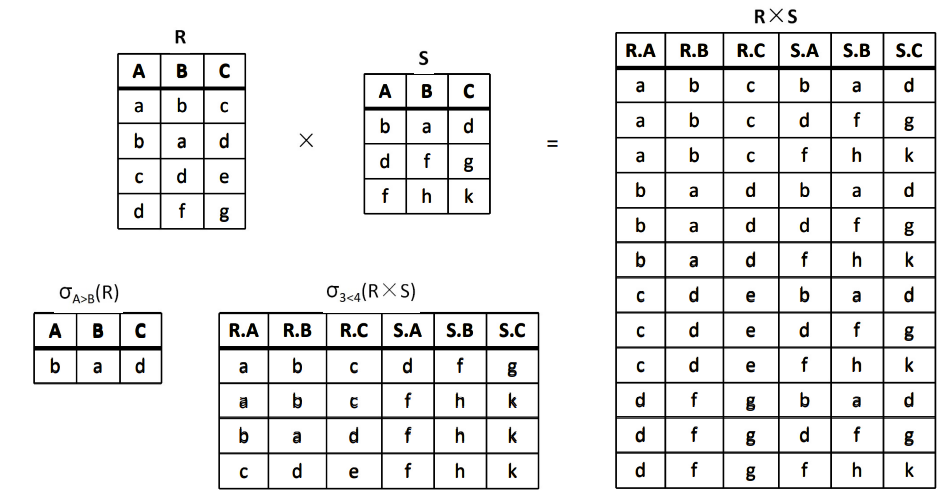
两个元数分别为 n 目和 m 目的关系 R 和 S 的广义笛卡儿积是一个 (n+m) 列的元组的集合。元组的前 n 列是关系 R 的一个元组,后 m 列是关系 S 的一个元组,记作 R×S。
投影及广义投影
投影是从关系的垂直方向进行运算,在关系R中选择出若干属性列 A 组成新的关系,记作 \Pi_A(R),其形式定义如下:
\Pi_A(R)=\{t[A]|t\in R\}
广义投影运算允许在投影列表中使用算术运算,实现了对投影运算的扩充。若有关系 R ,条件 F_1,F_2,…,F_n 中的每一个都是涉及 R 中常量和属性的算术表达式,那么广义投影运算的形式定义为:
\Pi_{F_1,F_2,…,F_n}(R)

选择
选择运算是从关系的水平方向进行运算,是从关系 R 中选择满足给定条件的诸元组,记作 σ_F(R),其形式定义如下:
σ_F(R)=\{t|t\in R\land F(T)=\mathrm{True}\}
其中,F 中的运算对象是属性名(或列的序号)或常数,运算符、算术比较符(<,\ >,\ ⩾,\ ⩽,\ ≠)和逻辑运算符(∧,\ ∨,\ ¬)。
例如,σ_{1⩾6}(R) 表示选取关系 R 中第 1 个属性值大于等于第 6 个属性值的元组;
σ_{1>’6′}(R)表示选取关系 R 中第 1 个属性值大于 6 的元组。
注意 6 和 ‘6’ 的区别,6 是指从左往右数第 6 个属性,‘6’ 是指数字 6(数值格式或文本格式)
例:设有关系 R,S 如下图所示,请求出 {R×S,\Pi_{A, C}(R), σ_{A>B}(R),σ_{3<4}(R×S)}
扩展的关系运算
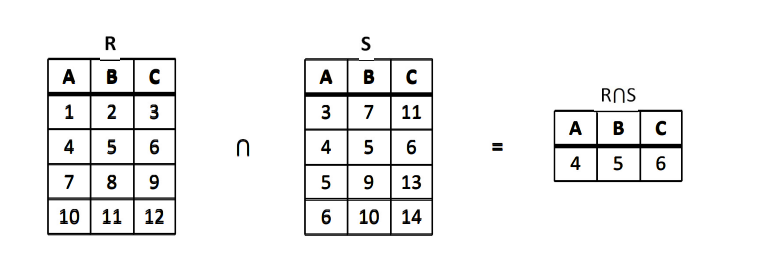
交
关系 R 与 S 具有相同的关系模式,关系 R 与 S 的交由属于 R 同时又属于 S 的元组构成,关系 R 与 S 的交记作 R\cap S,其形式定义如下:
R\cap S=\{t|t\in R\land t\in S\}
连接
分为 θ 连接、等值连接与自然连接
$θ$ 连接
可以由基本的关系运算笛卡儿积和选取运算导出。
R\bowtie_{XθY}S=σ_{XθY}(R×S)
其中,θ为比较运算符,如 >,<,=,≠,X 和 Y 分别为 R 和 S 上可以进行比较的属性组。
例:设有关系R 和 S 如下图所示,求R ⨝_{R.A<S.B}S
等值连接
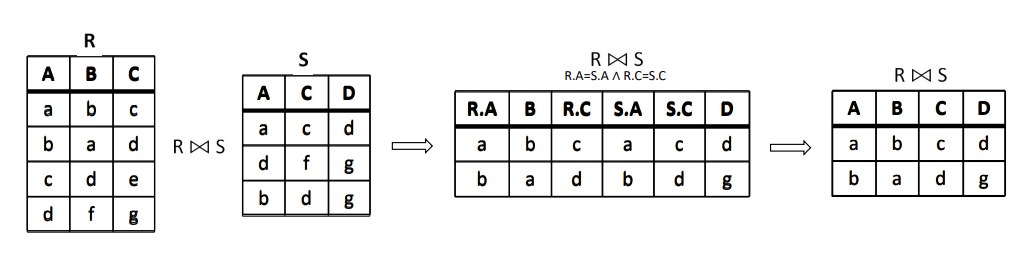
当 θ 为“=”时,称为等值连接,记为R⨝_{X=Y}S。
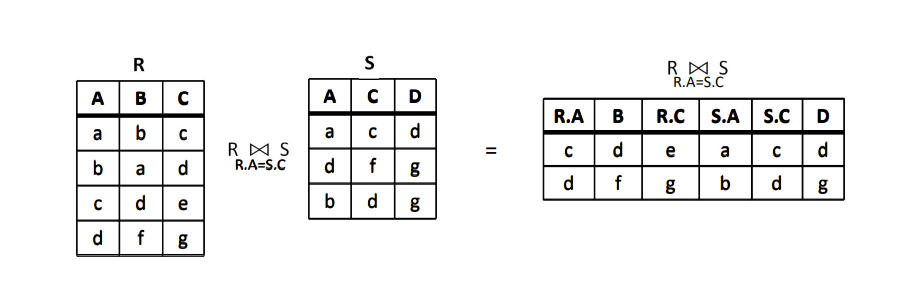
自然连接
是一种特殊的等值连接,它要求两个关系中进行比较的分量必须是相同的属性组,并且在结果集中将重复属性列去掉。如果没有重复属性,那么自然连接就转化为笛卡儿积。
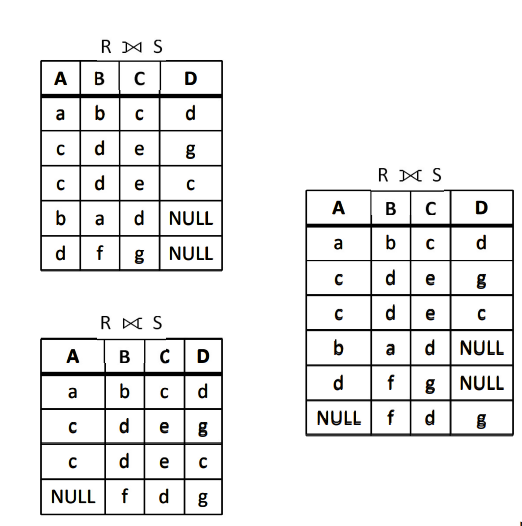
例:设有关系 R 与 S 如下图所示,求R⨝S。
除
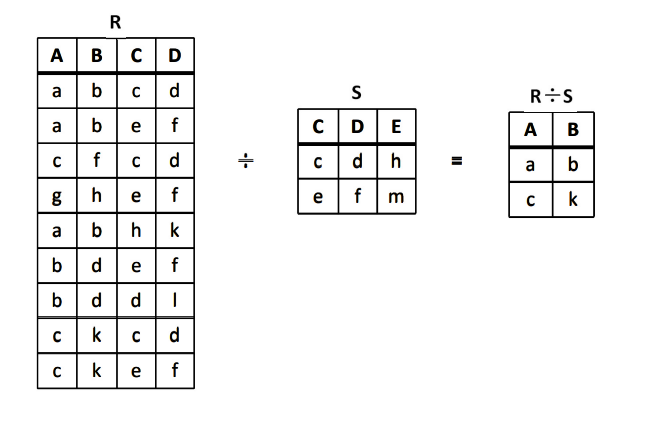
外连接
外连接运算是连接运算的扩展,可以处理缺失的信息。
左外连接 ⟕(左侧为准,右侧填充)
取出左侧关系中所有与右侧关系中任一元组都不匹配的元组,用空值 NULL 填充所有来自右侧关系的属性,构成新的元组,将其加入自然连接的结果中。
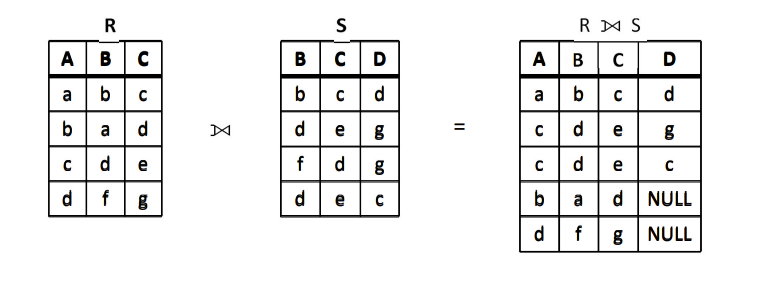
右外连接 ⟖(右侧为准,左侧填充)
取出右侧关系中所有与左侧关系中任一元组都不匹配的元组,用空值 NULL 填充所有来自左侧关系的属性,构成新的元组,将其加入自然连接的结果中。
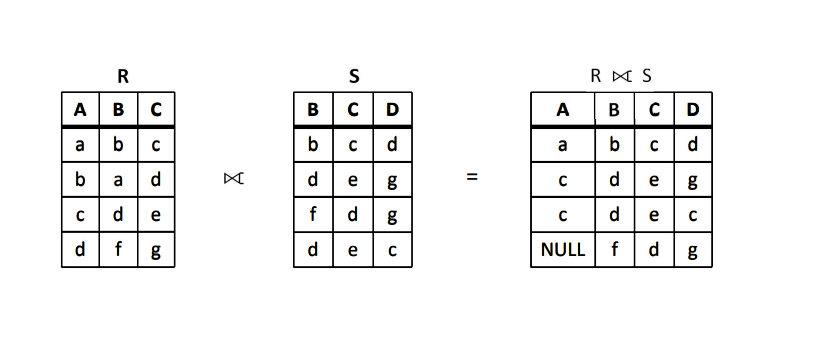
全外连接
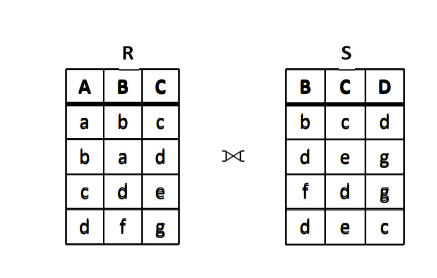
对关系运算的简单总结
| 关系运算 | 运算符 | 示例 | 一句话记忆 | 前提条件 |
|---|---|---|---|---|
| 并 | $\cup$ | $R\cup S$ | 在 R 中或者在 S 中的行 | $R$ 与 $S$ 的关系模式相同 |
| 差 | $-$ | $R-S$ | 在 R 中却不在 S 中的行 | $R$ 与 $S$的关系模式相同 |
| 交 | $\cap$ | $R\cup S$ | 既在 R 中又在S 中的行 | $R$ 与 $S$的关系模式相同 |
| 笛卡尔积 | $\times$ | $R\times S$ | ||
| 选择 | $\sigma$ | $\sigma_{1<3}(R)$ | 选择满足条件的行 | |
| 投影 | $\Pi$ | $\Pi_{A,B-C}(R)$ | 选择满足条件的列 | |
| 除 | $÷$ | $R÷S$ | ||
| $\theta$ 连接 | $\Join_{X\theta Y}$ | $R⨝_{X\theta Y}S$ | 先求出笛卡儿积,再做选择运算,选取满足“XθY”条件的行 | |
| 等值连接 | $\Join_{X=Y}$ | $R⨝_{X= Y}S$ | 先求出笛卡儿积,再做选择运算,选取满足“X=Y”条件的行 | |
| 自然连接 | $\Join$ | $R\Join S$ | $R$ 与 $S$ 进行等值连接时,比较的属性相同,且结果中要去掉重复属性列 | $R$ 与 $S$ 有相同的属性列 |
| 左外连接 | $⟕$ | $R ⟕ S$ | 在自然连接的基础上,以左侧为准,右侧补齐 | |
| 右外连接 | $⟖$ | $R⟖S$ | 在自然连接的基础上,以右侧为准,左侧补齐 | |
| 全外连接 | $⟗$ | $R⟗S$ | 将左外连接和右外连接的结果求并集 |
元组演算、域演算与查询优化
元祖演算
元组关系演算是非过程化查询语言,简称元组演算。它只描述所需信息,而不给出获得该信息的 具体过程。
在元组演算中,其元组演算表达式中的变量是以元组为单位的,其一般形式为:
\{t|P(t)\}
其中,t 是元组变量,P(t) 是元组演算公式,公式是由原子公式组成。
原子公式
- $R(t)$
$R$ 是关系名,$t$ 是元组变量,$R(t)$ 表示:$t$ 是关系 $R$ 中的一个元组。
-
$t[i]\ θ\ C$ 或 $C\ θ\ t[i]$
$t[i]$ 表示元组变量 $t$ 的第 $i$ 个分量,$C$ 是常量,$θ$ 为算术比较运算符。 -
$t[i]\ θ\ u[j]$
$t$ 和 $u$ 是两个元组变量。$t[i]\ θ\ u[j]$ 表示元组变量 $t$ 的第 $i$ 个分量与元组变量 $u$ 的第 $j$ 个分量之间满足 $θ$ 运算。
公式的定义
若一个公式的一个元组变量前有全称量词 ⩝ 或存在量词 ∃ 符号,则称该变量为约束变量,否则称之为自由变量。公式可递归定义如下:
- 原子公式是公式。
-
如果 φ1 和 φ2 是公式,那么,¬φ1,φ1∨φ2,φ1∧φ2,φ1⇒φ2 也都是公式。分别表示如下命题: ¬φ1 表示“φ1 不为真”,φ1∨φ2 表示“φ1 或φ2 为真”,φ1∧φ2 表示“φ1 和 φ2 都为真”;φ1⇒φ2表示“若 φ1 为真则 φ2 为真”。
-
如果是 φ1 公式,那么,∃t(φ1) 是公式。∃t(φ1) 表示这样一个命题: “如果有一个 t 使 φ1 为真,则∃t(φ1) 为真,否则 ∃t(φ1) 为假”。
-
如果是 φ1 公式,那么,⩝t(φ1) 是公式。⩝t(φ1) 表示这样一个命题: “如果对所有的 t 使 φ1 为真,则⩝t(φ1)为真,否则 ⩝t(φ1)为假”。
公式中运算符的优先顺序为:
θ > ⩝ 和 ∃ > ¬ > ∧ 和 ∨ > ⇒,加括号时,括号中的运算符优先。
例:设有关系 R、S 如下图所示,对如下所示的元组演算表达式,求出它们的值。
- $R1 = \{ t | R(t) ∧ ¬S(t) \}$
- $R2 = \{ t | S(t) ∧ t[3]>t[2] ∧ t[2]<8 \}$
- $R3 = \{ t | (∃u) (R(t) ∧ S(u) ∧ t[3]<u[2]) \}$
- $R4 = \{ t | (⩝u) (R(t) ∧ S(u) ∧ t[3]>u[1]) \}$
- $R5 = \{ t | (∃u) (∃v) (R(u) ∧ S(v) ∧ u[2]>v[1] ∧ t[1]=u[1] ∧ t[2]=v[1] ∧ t[3]=v[3]) \}$
R 表格如下:
A B C 1 2 3 4 5 6 7 8 9 10 11 12 S 表格如下:
A B C 3 7 11 4 5 6 5 9 13 6 10 14 则有 R1:
A B C 1 2 3 7 8 9 10 11 12 R2:
A B C 3 7 11 4 5 6 R3:∃u 表示:只要有一个(存在一个)u 使得后面的公式成立就可以了,即 t[3] 只要小于 u[2] 中的其中一个就可以了,如果 t[3]⩾ 所有的 u[2],就说明不存在任何一个 u 满足条件。
A B C 1 2 3 4 5 6 7 8 9 R4:对任意一个(所有的)u,都要使后面的公式成立,只要有一个 u 没有满足这个条件,就不行。即:满足条件的t[3] 应该大于所有的 u[1]。
A B C 7 8 9 10 11 12 R5
R.A S.A S.C 4 3 11 4 4 6 7 3 11 7 4 6 7 5 13 7 6 14 10 3 11 10 4 6 10 5 13 10 6 14
域演算
域关系演算简称域演算。在域演算中,表达式中的变量是表示域的变量,可将关系的属性名视为 域变量,域演算表达式的一般形式为
\{t_1,…,t_k|P(t_1,…,t_k)\}
其中,t_1,…,t_k 是域变量,P(t_1,…,t_k) 是域演算公式。
原子公式
- $R(t_1,…,t_i,…,t_k)$
$R$ 是 $k$ 元关系,$t_i$ 是元组变量 $t$ 的第 $i$ 个分量,$R(t_1,…,t_i,…,t_k)$表示这样一个命题: 以$t_1,…,t_i,…,t_k$为分量的元组在关系$R$。
-
$t_iθC$ 或 $Cθt_i$
$t_i$ 表示元组变量 $t$ 的第 $i$ 个分量,$C$ 是常量,$θ$ 为算术比较运算符。
-
$t_iθu_j$
$t_i$ 和 $u_j$ 是两个域变量。$t_iθ u_j$ 表示元组变量 $t$ 的第 $i$ 个分量与元组变量 $u$ 的第 $j$ 个分量之间满足 $θ$ 运算。
公式的定义
若一个公式的一个元组变量前有全称量词 ⩝ 或存在量词 ∃ 符号,则称该变量为约束变量,否 则称之为自由变量。
公式可递归定义如下:
- 原子公式是公式。
- 如果 φ1和 φ2 是公式,那么,¬φ1,φ1∨φ2,φ1∧φ2,φ1⇒φ2 也都是公式。
- 如果是 φ1 公式,那么,∃t_i(φ_1) 是公式。∃t_i(φ_1) 表示这样一个命题: “如果有一个 t_i 使 φ_1 为真,则 ∃t_i(φ_1) 为真,否则 ∃t_i(φ_1) 为假”。
- 如果 φ_1(t_1,…,t_i,…,t_k) 是公式,那么,⩝t_i(φ_1) 是公式。⩝t(φ_1) 表示这样一个命题: “如果对所有的 t_i 使 φ_1(t_1,…,t_i,…,t_k) 为真,则 ⩝t_i(φ_1) 为真,否则 ⩝t_i(φ_1) 为假”。
公式中运算符的优先顺序为: θ > ⩝ 和 ∃ > ¬ > ∧ 和 ∨ > ⇒,加括号时,括号中的运算符优先。
例:设有关系 R、S 如下图所示,对如下所示的域演算表达式,求出它们的值。
- $R_1 = \{ t_1 t_2 t_3 | R (t_1 t_2t_3) ∧ t_1 < t_2 ∧ t_2 > t_3 \}$
- $R_2 = \{ t_1t_2t_3 | ( R (t_1t_2t_3) ∧ t_1>4 ) ∨ ( S (t_1t_2t_3) ∧ t_2<8) \}$
- $R_3 = \{ t_1t_2t_3 | (∃u)(∃v)(∃w) R(ut_2v) ∧ S(t_1wt_3) ∧ u⩾7 ∧ v>w \}$
R:
A B C 1 2 1 4 5 7 7 8 6 10 11 9 S:
A B C 1 2 3 4 5 6 7 8 8 10 11 11 R_1:
A B C 1 2 1 7 8 6 10 11 9 R_2:
A B C 7 8 6 10 11 9 1 2 3 4 5 6 R_3:
S.A R.B S.C 1 8 3 4 8 6 1 11 3 4 11 6 7 11 9
查询优化
查询优化是指为查询选择最有效的查询计划的过程。一个查询可能会有多种实现方法,关键是如 何找出一个与之等价的且操作时间又少的表达式,以节省时间、空间,提高查询效率。
在关系代数运算中,笛卡儿积、连接运算是最耗费时间和空间的。
优化的准则:
- 提早执行选取运算。对于有选择运算的表达式,应优化成尽可能先执行选择运算的等价表达式, 以得到较小的中间结果,减少运算量和从外存读块的次数。
- 合并乘积与其后的选择运算为连接运算。
- 将投影运算与其后的其他运算同时进行,以避免重复扫描关系。
- 将投影运算和其前后的二目运算结合起来,使得没有必要为去掉某些字段再扫描一遍关系。
- 在执行连接前对关系适当地预处理,就能快速地找到要连接的元组。方法有两种:索引连接法、 排序合并连接法。
- 存储公共子表达式。对于有公共子表达式的结果应存于外存(中间结果),这样,当从外存读 出它的时间比计算的时间少时,就可节约操作时间。
例:供应商数据库中有:供应商 S、零件 P 、项目 J 、供应 SPJ 四个基本表(关系),其关系模式如 下所示:
\text{S (Sno, Sname, Status, City)} 供应商编号,供应商名称,供应商城市
\text{P (Pno, Pname, Color, Weight)} 零件号,零件名称,颜色,重量
\text{J (Jno, Jname, City)}工程号,项目名称,所在城市
\text{SPJ (Sno, Pno, Jno, Qty)} 供应商编号,零件编号,工程号,数量
若用户要求查询使用“上海”供应商生产的“红色”零件的工程号,请解答如下问题:
- 试写出该查询的关系代数表达式;
\pi_{Jno}(σ_{City=’上海’∧Color=’红’}(S⨝SPJ⨝P) )
- 试写出查询优化的关系代数表达式。
\pi_{Jno}(\pi_{Sno}(\sigma _{city = ‘上海'(S)}) \Join \pi_{Sno, Pno, Jno} (SPJ) \Join \pi_{Pno} ( \sigma_{Color} = ‘红’ (P)))
- 画出该查询初始的关系代数表达式的语法树。
- 使用优化算法,对语法树进行优化,并画出优化后的语法树。
关系数据库设计基础知识
函数依赖
定义:设 R(U) 是属性集 U 上的关系模式,X、Y 是 U 的子集。**若对 R(U) 的任何一个可能的关系 r **,r 中不可能存在两个元组在 X 上的属性值相等,而在 Y 上的属性值不等, 则称 X 函数决定 Y 或 Y 函数依赖于 X ,记作:X→Y
- 如果 X→Y,那么对于任意两个相同的 X,所对应的 Y 是一定相同的。
-
如果 X→Y,但 Y⊈X,则称 X→Y 是非平凡的函数依赖。一般情况下总是讨论非平凡 的函数依赖。
-
如果 X→Y,但 Y⊆X,则称 X→Y 是平凡的函数依赖。
函数依赖的定义要求关系模式 R 的任何可能的 r 都满足上述条件。因此不能仅考察关系模式 R 在某一时刻的关系 r,就断定某函数依赖成立。
函数依赖是语义范畴的概念,我们只能根据语义来确定函数依赖。
完全函数依赖与部分函数依赖
定义:在 R(U) 中,如果 X→Y,并且对于 X 的任何一个真子集X’,都有 X’ 不能决定 Y ,则称 Y 对 X 完全函数依赖,记作:X→Y。如果 X→Y,但 Y 不完全函数依赖于 X ,则称 Y 对 X 部分函数依赖,记作:X→Y。部分函数依赖也称局部函数依赖
例:选课关系 SC1(\underline{学号,课程号},成绩),F={(学号,课程号)→ 成绩}
则有 (学号,课程号)→ 成绩,学号⇸成绩,课程号⇸成绩。
选课关系SC2(\underline{学号,课程号},学生姓名,课程名称,成绩),F={(学号,课程号)
→ 成绩,(学号,课程号)→ 课程名称,(学号,课程号)→ 学生姓名,学号→学生 姓名,课程号 → 课程名称}。
传递函数依赖
定义:在 R(U,F) 中,如果 X→Y,Y→Z,Y⊈X,Y⇸X,则称 Z 对 X 传递依赖。
例:\text{供应商(Sno,Sname,Status,City,Pno,Qty)},及函数依赖集如下,判断该关系是否存在传递函数依赖和部分函数依赖。
\text{F={Sno→Sname, Sno→Status, Status→City,(Sno,Pno)→Qty}}
码
候选码和主码
设 K 为 R(U,F) 中的属性的组合,若 K→U,且对于 K 的任何一个真子集 K’,都有 K’ 不 能决定 U ,则 K 为 R 的候选码,若有多个候选码,则选一个作为主码。
- 候选码通常也可以称为候选关键字,主码通常也可以称为主关键字或主键。
- 包含在任何一个候选码中的属性叫做主属性,否则叫做非主属性。
例:\text{选课关系SC1(Sno,Cno,Sname,Cname,G)}
\text{选课关系SC2(Sno,Cno,Sname,Cname)}
外码
若 R(U) 中的属性或属性组 X 非 R 的码,但 X 是另一个关系的码,则称 X 是 R 的 外码(Foreign Key)或称外键。
例:学生(学号,姓名,班主任,所属学院)
教师(职工号,姓名)
学院(编号,名称)
多值依赖
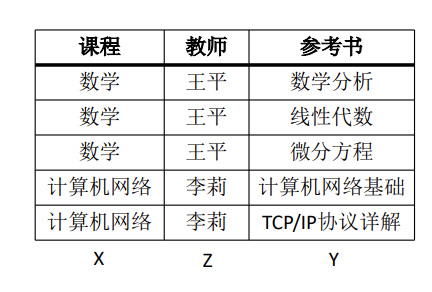
定义:若关系模式 R(U) 中,X,Y,Z 是 U 的子集,并且 Z=U-X-Y。当且仅当对 R(U) 的任何一个关系 r,给定一对 (x,z) 值,有一组 Y 的值,这组值仅仅决定于 x 值而与 z 值无关,则称“Y 多值依赖于 X ”或“X 多值决定 Y ”成立。记为: X→→Y
例:参考书目(课程,教师,参考书)
课程 →→ 参考书
如果 Z=∅,为平凡的多值依赖;
如果 Z≠∅,则为非平凡的多值依赖。
多值依赖具有如下 6 条性质:
- 多值依赖具有对称性。即若 X→→Y,则 X→→Z,其中Z=U-X-Y。
- 多值依赖的传递性。即若 X→→Y,Y→→Z,则 X→→Z-Y。
- 函数依赖可以看成是多值依赖的特殊情况。
- 若 X→→Y,X→→Z,则 X→→YZ。
- 若 X→→Y,X→→Z,则 X→→Y ⋂Z。
- 若 X→→Y,X→→Z,则 X→→Z-Y。