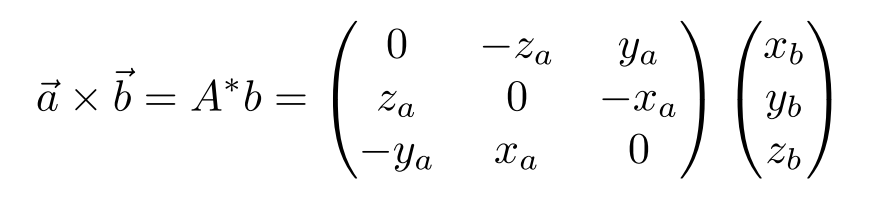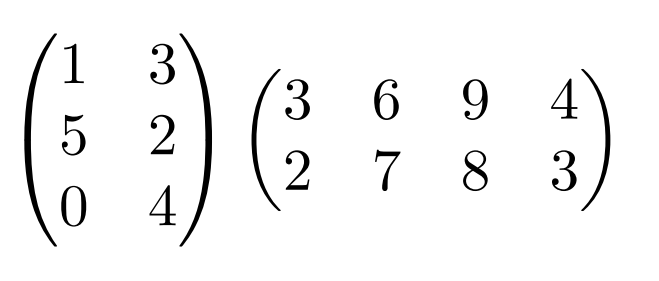向量
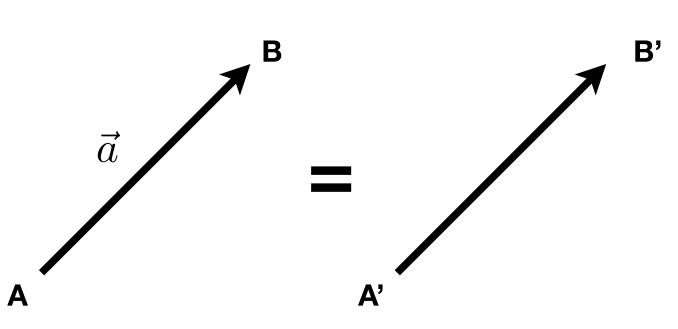
- 通常写作 \vec{a} 或者加粗的 a
- 或者使用起点和终点的形式 \overrightarrow{AB}=B-A
- 有距离和长度
- 没有具体的起点位置
向量归一化
- 向量的大小(长度)写为 \left | \vec{a} \right |
-
单位向量
- 大小为 1 的向量
- 求向量的单位向量(归一化):\hat{a} =\frac{\vec{a} }{\left | \vec{a} \right |}
- 用于表示方向
向量加法
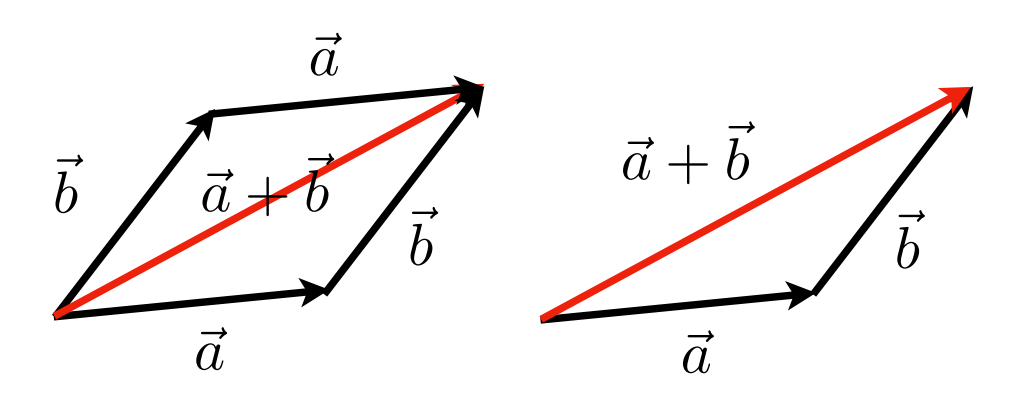
- 几何:平行四边形定律和三角形定律
- 代数:简单地添加坐标
笛卡尔坐标
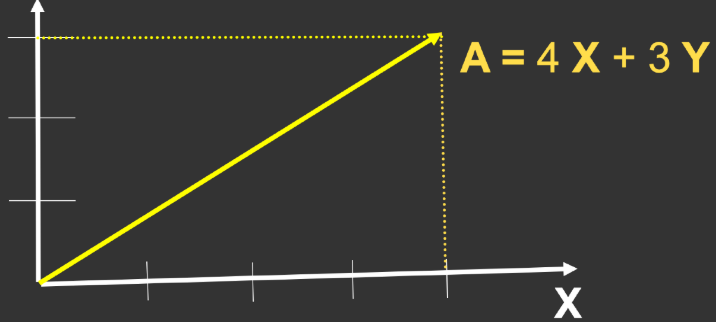
X 和 Y 可以是任何(通常是正交单位)向量
A=\begin{pmatrix}
x \\ y
\end{pmatrix}\\
A^T=(x,y)\\
\left |A\right |=\sqrt{x^2+y^2}
向量乘法
点乘
点(标量)积
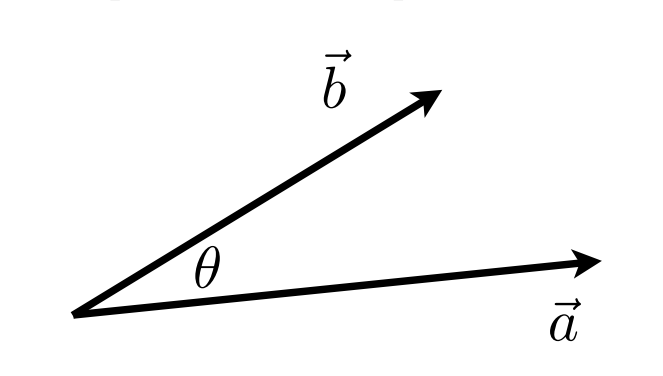
\vec{a}\cdot\vec{b}=\left |\vec{a}\right |\left |\vec{b}\right |\cos\theta\\
\cos\theta=\frac{\vec{a}\cdot\vec{b}}{\left |\vec{a}\right |\left |\vec{b}\right |}
对于单位向量,有
\cos\theta=\hat{a}\cdot\hat{b}
特性
\vec{a}\cdot\vec{b}=\vec{b}\cdot\vec{a}\\
\vec{a}\cdot(\vec{b}+\vec{c})=\vec{a}\cdot\vec{b}+\vec{a}\cdot\vec{c}\\
(k\vec{a})\cdot\vec{b}=\vec{a}\cdot(k\vec{b})=k(\vec{a}\cdot\vec{b})
笛卡尔坐标中的点积
逐个乘法,然后相加
- 2D
\vec{a}\cdot\vec{b}=\begin{pmatrix} x_a\\y_a\end{pmatrix}\cdot\begin{pmatrix} x_b\\y_b\end{pmatrix}=x_ax_b+y_ay_b -
3D
\vec{a}\cdot\vec{b}=\begin{pmatrix} x_a \\ y_a\\z_a\end{pmatrix}\cdot\begin{pmatrix} x_b \\y_b\\z_b\end{pmatrix}=x_ax_b+y_ay_b+z_az_b
图形中的点积
- 查找两个向量之间的角度(例如光源和表面之间角度的余弦)
- 寻找一个向量在另一个向量上的投影
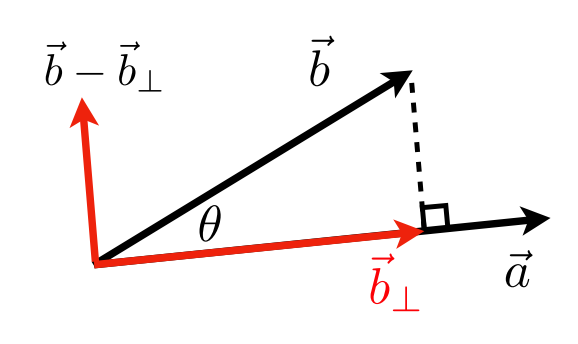
投影点积
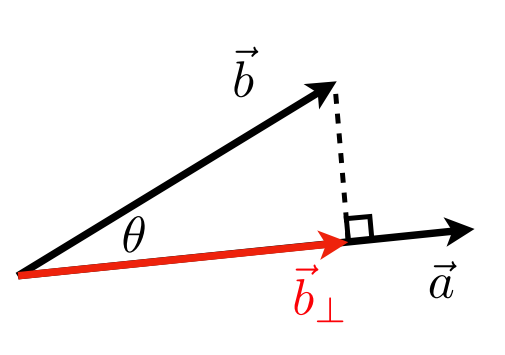
- $\vec{b}_{\bot} $:$\vec{b}$ 到 $\vec{a}$ 上的投影
- $\vec{b}_{\bot} $必须沿着 $\vec{a}$ (或者沿着$\hat{a}$)
- $\vec{b}_{\bot}=k\hat{a}$
- 它的大小为 k
- $\vec{b}_{\bot} $必须沿着 $\vec{a}$ (或者沿着$\hat{a}$)
- $k=\left |\vec{b}_{\bot}\right |=\left |\vec{b}\right |\cos\theta$
图形中的点积
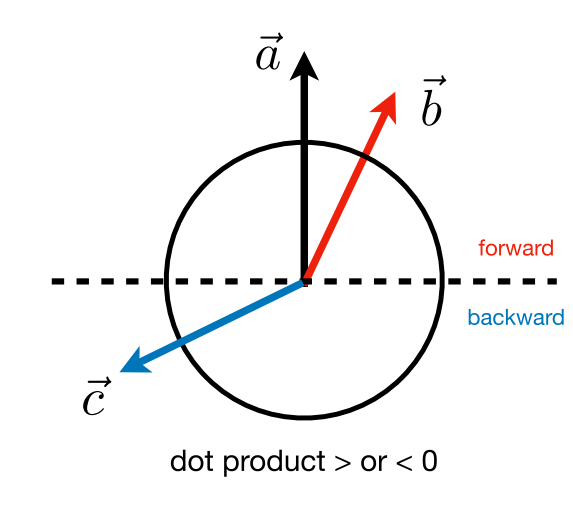
- 测量两个方向的距离
- 分解向量
- 确定正面/背面
叉乘
叉(矢量)乘
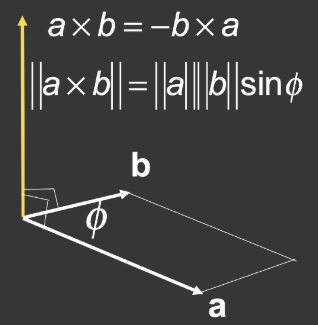
- 叉积与两个初始向量正交
- 方向由右手定则确定
- 用于构建坐标系
叉积的性质
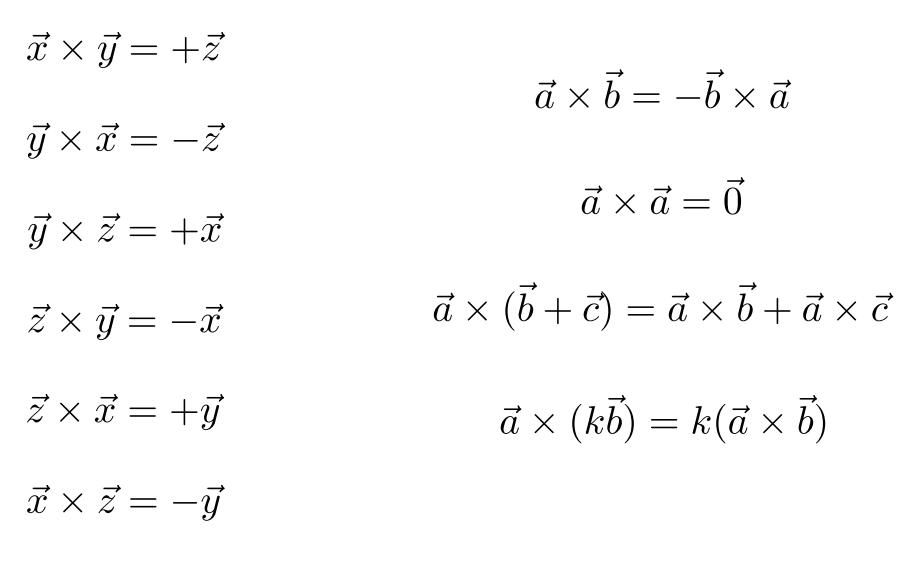
叉积的笛卡尔公式
\vec{a}\times\vec{b}=\begin{pmatrix}y_az_b-y_bz_a\\z_ax_b-x_az_b\\x_ay_b-y_ax_b\end{pmatrix}
向量 a 的对偶矩阵
\vec{a}\times\vec{b}=\begin{pmatrix}0&-z_a&y_a\\z_a&0&-x_a\\-y_a&x_a&0\end{pmatrix}\begin{pmatrix}x_b\\y_b\\z_b\end{pmatrix}
图形学中的叉积

- 确定左/右方向
- 确定前/后方向
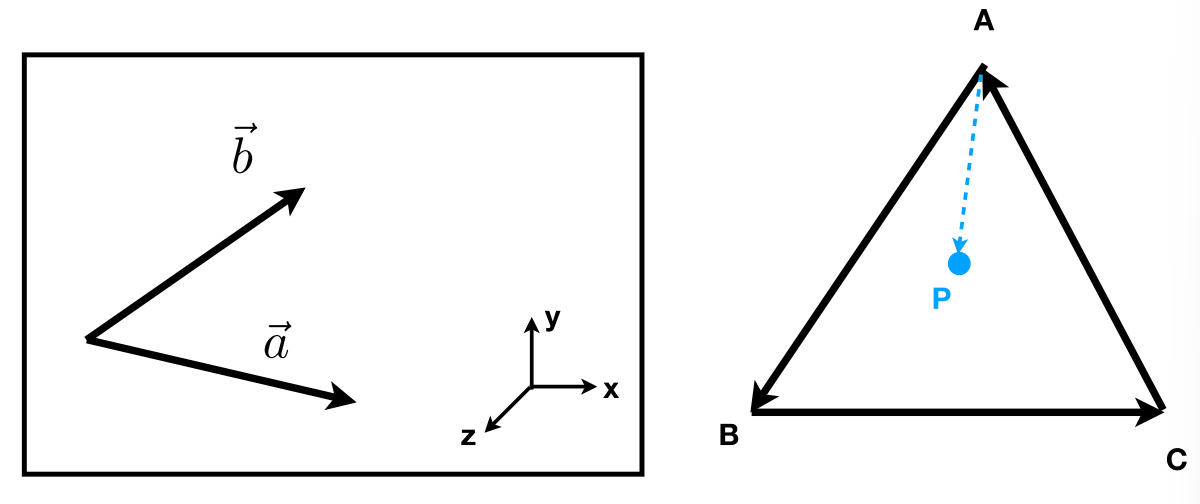
- 判定 b 在 a 左侧还是右侧
z 轴是正数,所以叉乘大于 0 的话在左侧。
- $a\times b >0$,左侧
– a\times b<0,右侧
z 轴朝向屏幕外是正方向,摄像机前向是 z 轴负方向
- 判定p点是否在三角形内部(向外朝向屏幕外,就是不指向屏幕)
- AB 叉乘 AP ,向外 — P在AB左侧
BC 叉乘 BP,向外 — P在BC左侧
CA 叉乘 CP,向外 — P在CA左侧
综合,P在三角形内部
只有全是左侧或者右侧才能判定点在三角形内侧
正交基和坐标系
正交基/坐标系
- 对于表示点、坐标、位置很重要
- 通常,多组坐标系
- 全局、局部、世界、模型、模型的一部分(头、手……)
- 关键问题是这些系统/基础之间的转换
正交坐标系
在任何一组 3 个向量(在 3D 中)

矩阵
什么是矩阵
- 数字数组(m × n = m 行,n 列)
\begin{pmatrix}1&2 \\ 3&4 \\5&6\end{pmatrix}
- 标量的加法和乘法是微不足道的:逐个元素
矩阵-矩阵乘法
- A 中的#(数量)列必须 = B 中的 # 行 (M\times N) (N \times P) = (M \times P)
-
乘积中的元素 (i, j) 是来自 A 的 i 行和来自 B 的 j 列的点积
-
性质
- 无交换律(AB和BA一般不一样)
- 结合律和分配率
- $(AB)C=A(BC)$
- $A(B+C)=AB+AC$
- $(A+B)C=AC+BC$
- 将向量视为列矩阵 (m×1)
-
转换的关键
-
关于 y 轴的 2D 反射
\begin{pmatrix}-1&0\\0&1 \end{pmatrix}\begin{pmatrix}x\\y \end{pmatrix}=\begin{pmatrix}-x\\y \end{pmatrix}
矩阵变换
- 切换行和列(ij \rightarrow ji)

- 性质
(AB)^T=B^TA^T
单位矩阵和逆
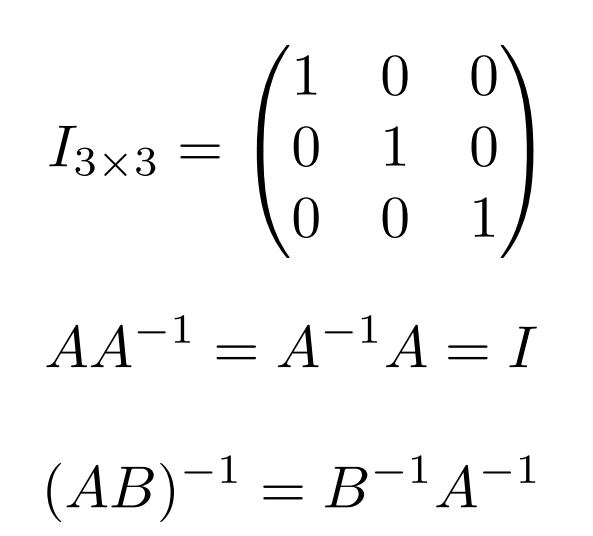
矩阵形式的向量乘法
点乘
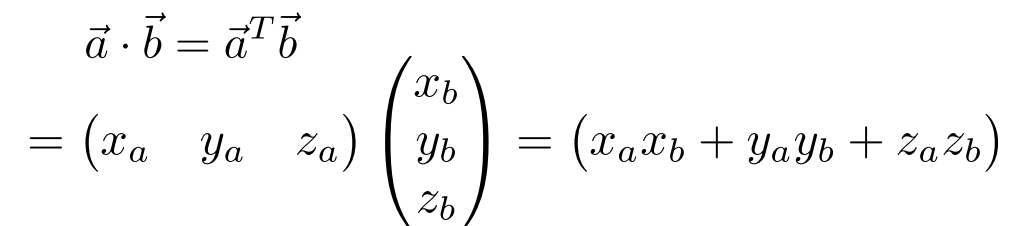
叉乘