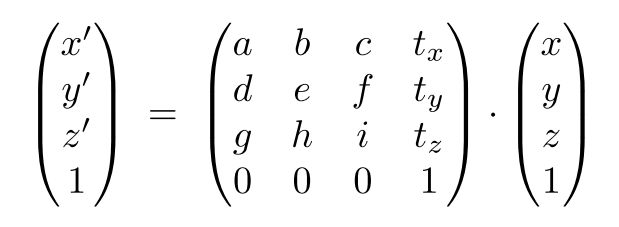2D 变换
线性变换
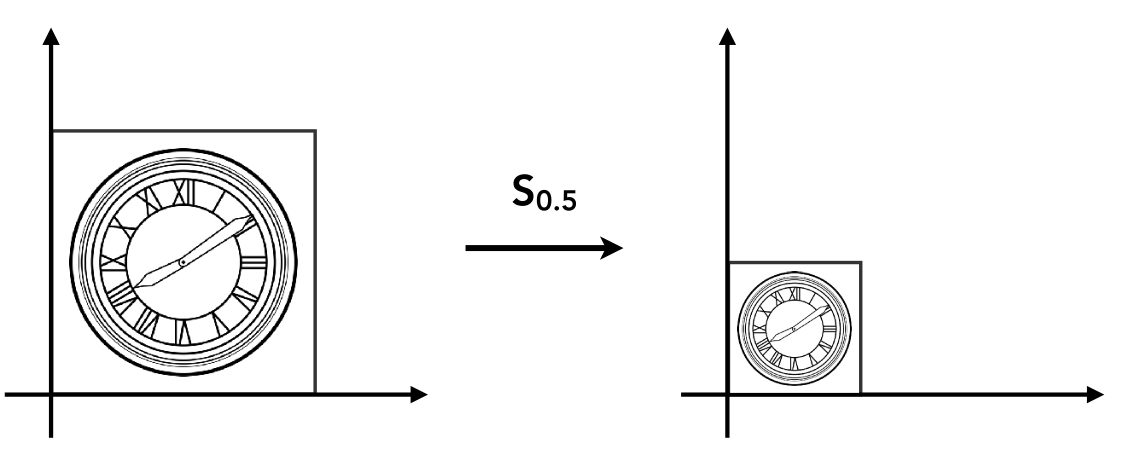
比例变换
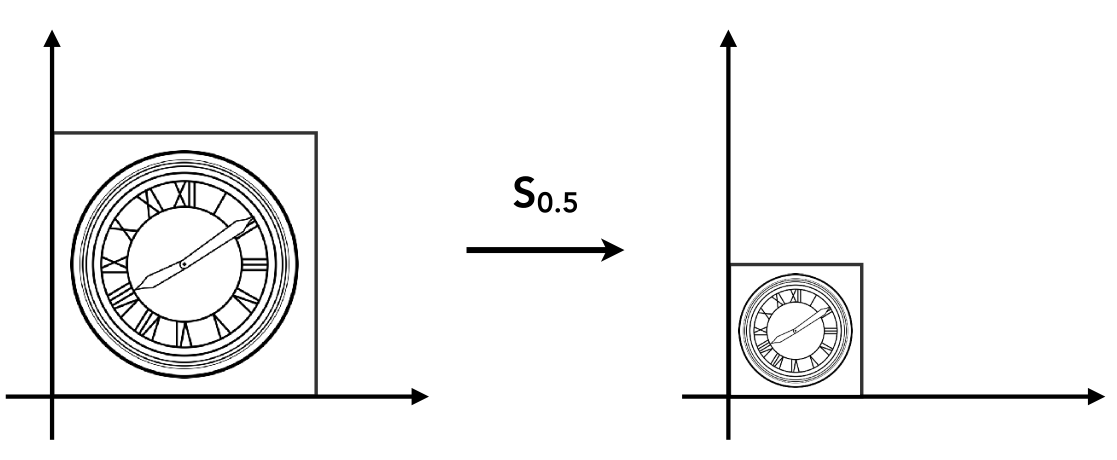
x^\prime =sx\\
y^\prime =sy
比例矩阵
\begin{bmatrix} x^\prime \\y^\prime \end{bmatrix}=\begin{bmatrix} s&0 \\0&s\end{bmatrix}\begin{bmatrix} x \\y \end{bmatrix}
比例矩阵(非均匀)
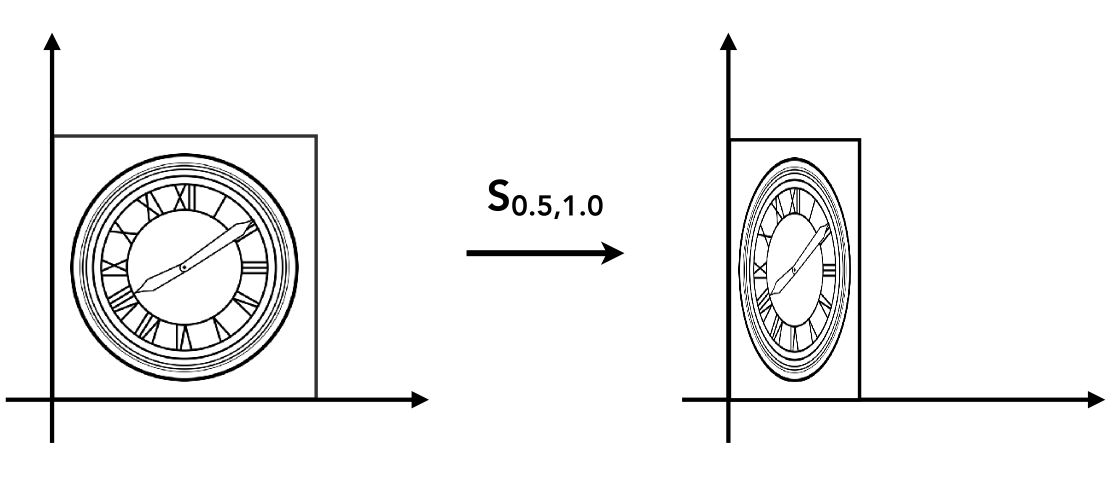
\begin{bmatrix} x^\prime \\y^\prime \end{bmatrix}=\begin{bmatrix} s_x&0 \\0&s_y\end{bmatrix}\begin{bmatrix} x \\y \end{bmatrix}
反射矩阵
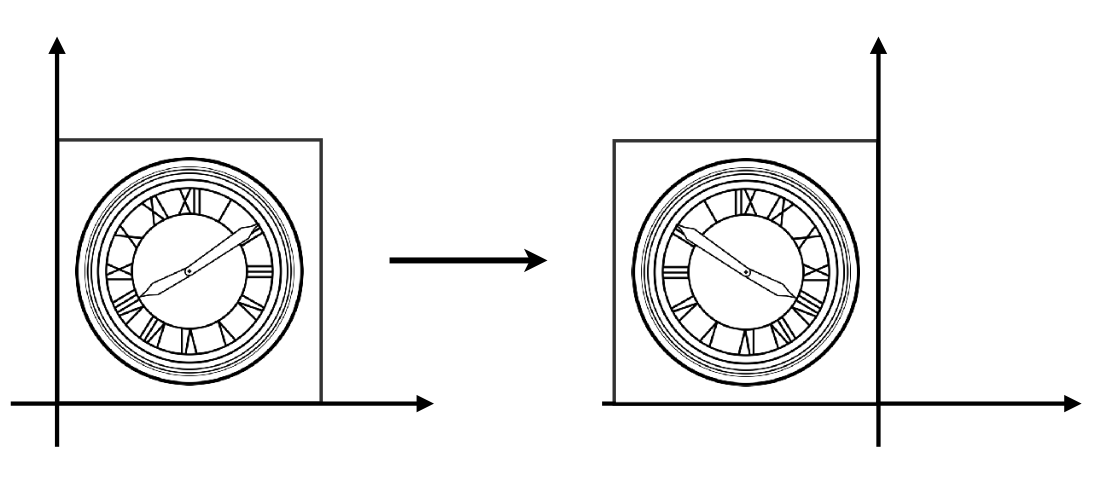
水平反射
x^\prime =-x\\
y^\prime =y
\begin{bmatrix} x^\prime \\y^\prime \end{bmatrix}=\begin{bmatrix} -1&0 \\0&1\end{bmatrix}\begin{bmatrix} x \\y \end{bmatrix}
剪切矩阵
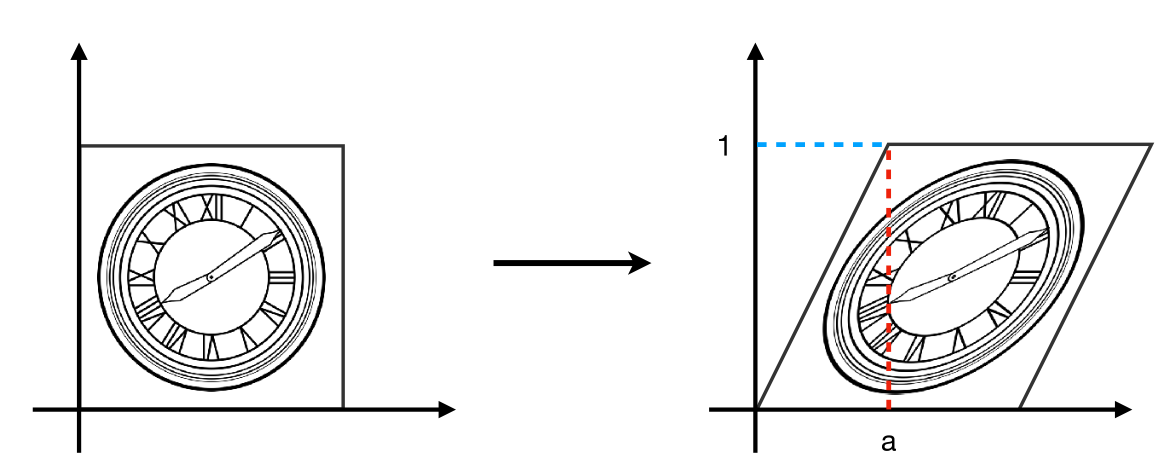
在 y=0 时水平移位为 0
在 y=1 时水平移位为 a
垂直移位始终为 0
\begin{bmatrix} x^\prime \\y^\prime \end{bmatrix}=\begin{bmatrix} 1&a \\0&1\end{bmatrix}\begin{bmatrix} x \\y \end{bmatrix}
旋转矩阵
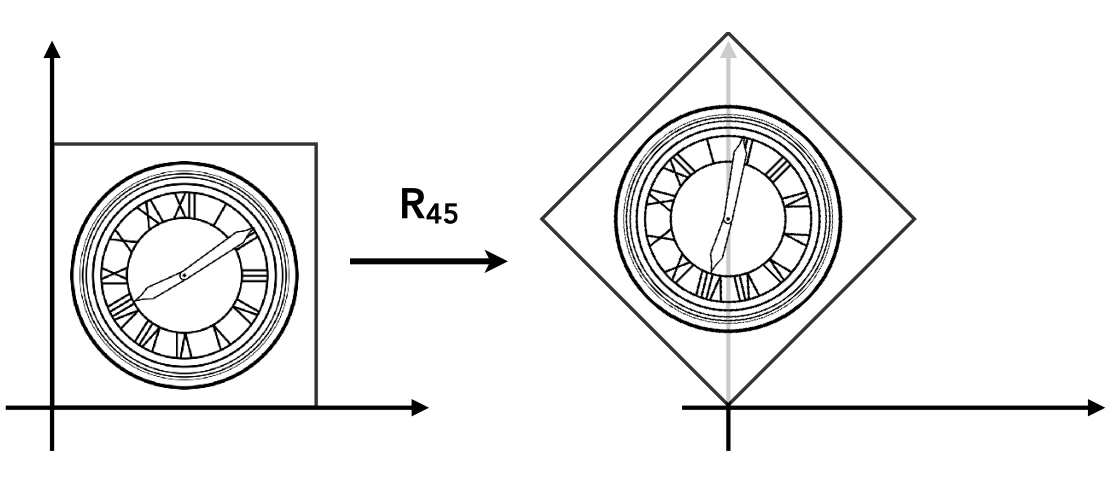
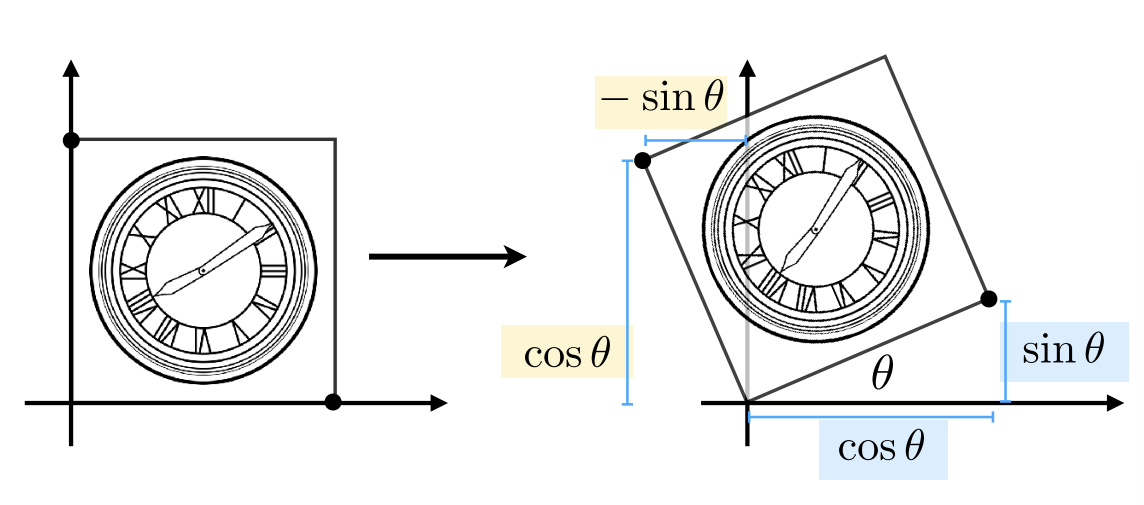
R_\theta=\begin{bmatrix} \cos\theta&-\sin\theta \\ \sin\theta&\cos\theta \end{bmatrix}
相同维度线性变化
x^\prime=ax+by\\
y^\prime=cx+dy\\
\begin{bmatrix} x^\prime \\y^\prime \end{bmatrix}=\begin{bmatrix} a&b \\c&d\end{bmatrix}\begin{bmatrix} x \\y \end{bmatrix}\\
x^\prime=Mx
齐次坐标
添加第三个坐标,有点 (x,y,1)^T ,向量 (x,y,0)^T ,则有:
- 点-点=向量
- 向量 向量=向量
- 点+向量=点
- 点+点=两点的中点
在齐次坐标中,\begin{pmatrix}x \\y\\w\end{pmatrix} 都视作\begin{pmatrix}x/w \\y/w\\1\end{pmatrix},其中 w\not=0
仿射变换
仿射变化=线性变换+平移
\begin{pmatrix}x^\prime \\y^\prime\end{pmatrix}=\begin{pmatrix}a&b \\c&d\end{pmatrix}\cdot\begin{pmatrix}x \\y\end{pmatrix}+\begin{pmatrix}t_x \\t_y\end{pmatrix}
使用齐次坐标
\begin{pmatrix}x^\prime \\y^\prime\\1\end{pmatrix}=\begin{pmatrix}a&b&t_x \\c&d&t_y\\0&0&1\end{pmatrix}\cdot\begin{pmatrix}x\\y\\1\end{pmatrix}
平移
\mathbf{S} (s_x,s_y)=\begin{pmatrix}s_x&0&0 \\0&s_y&0\\0&0&1\end{pmatrix}
旋转
\mathbf{R} (\alpha)=\begin{pmatrix}\cos\alpha&-\sin\alpha&0 \\\sin\alpha&\cos\alpha&0\\0&0&1\end{pmatrix}
变换
\mathbf{R} (\alpha)=\begin{pmatrix}1&0&t_x \\ 0&1&t_y\\0&0&1\end{pmatrix}
逆变换
M^{-1} 是矩阵 M 在几何意义上的变换的逆
变换合成
矩阵相乘不满足结合律,例如,先旋转再平移和先平移再旋转所得结果不一样
仿射变换序列\mathbf{A_1},\mathbf{A_2},\mathbf{A_3}……
- 通过矩阵乘法组成
- 对性能非常重要
- 预乘 n 个矩阵以获得表示组合变换的单个矩阵
A_n(…A_2(A_1(x)))=\mathbf{A_n}…\mathbf{A_2A_1}\cdot\begin{pmatrix}x\\y\\1\end{pmatrix}
分解复杂的变换
如何围绕给定点 c 旋转?
- 将中心平移到原点
- 旋转
- 向后平移
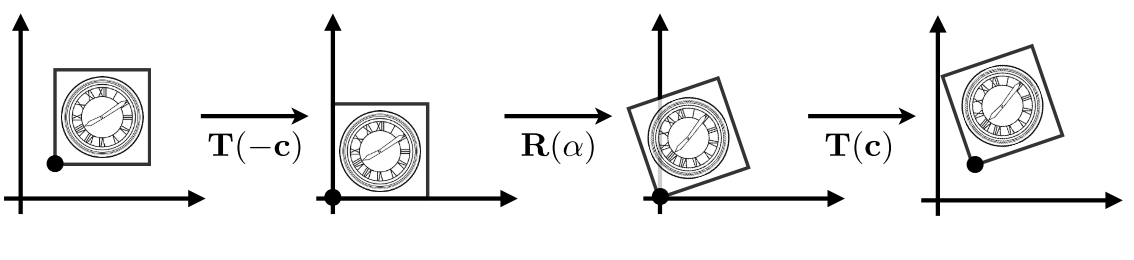
\mathbf{T(c)\cdot R(\alpha)\cdot T(-c)}
3D变换
3D也使用齐次坐标:
- 3D 的点:(x,y,z,1)^T
- 3D 的向量:(x,y,z,0)^T
通常,(x,y,z,w) 是一个 3D 点 (x/w,y/w,z/w)
3D变换通常使用 4×4 矩阵进行仿射变换