3D 变换

平移

T(t_x,t_y,t_z)=\begin{pmatrix}
1 & 0&0 &t_x \\
0 &1&0&t_y\\
0 &0 &1 &t_z \\
0 &0 &0 &1
\end{pmatrix}

缩放

S(s_x,s_y,s_z)=\begin{pmatrix}
s_x & 0&0 &0 \\
0 &s_y&0&0\\
0 &0 &s_z &0 \\
0 &0 &0 &1
\end{pmatrix}

旋转

R_x(\alpha)=\begin{pmatrix}
1 & 0&0 &0 \\
0 &\cos\alpha&-\sin\alpha&0\\
0 &\sin\alpha &\cos\alpha &0 \\
0 &0 &0 &1
\end{pmatrix}\\
R_y(\alpha)=\begin{pmatrix}
\cos\alpha & 0&\sin\alpha &0 \\
0 &1&0&0\\
-\sin\alpha &0 &\cos\alpha &0 \\
0 &0 &0 &1
\end{pmatrix}\\
R_z(\alpha)=\begin{pmatrix}
\cos\alpha & -\sin\alpha&0 &0 \\
\sin\alpha &\cos\alpha&0&0\\
0 &0 &1 &0 \\
0 &0 &0 &1
\end{pmatrix}

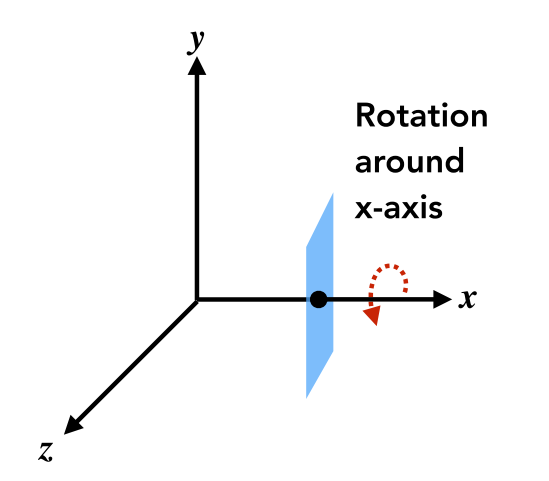
3D 旋转变换矩阵遵循循环对称：X\times Y=Z,Y\times Z=X,Z\times X=Y

合成的旋转变换

R_{xyz}(\alpha,\beta,\gamma)=R_x(\alpha)R_y(\beta)R_z(\gamma)

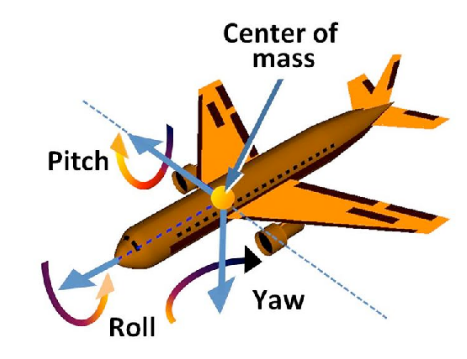
• 称为“欧拉角”
• 常用于飞行模拟器：roll、pitch、yaw

罗德里格斯旋转公式

绕旋转轴 n 旋转 \alpha 角度
R(n,\alpha)=\cos(\alpha)I+(1-\cos(\alpha))nn^T+\sin(\alpha)N\\
N=\begin{pmatrix}
0 & -n_z&n_y \\
n_z &0&-n_x\\
-n_y &n_x &0 \\
\end{pmatrix}

四元数：旋转与旋转之间的差值

推导过程

1. 对 v 做正交分解，得：v=v_\parallel+v_\perp

2. 由向量的矢量投影公式，得：v_\parallel=(v\cdot k)\cdot k

3. 由 ① 和 ② ，得：v_\perp=v-v_\parallel=v-(v\cdot k)\cdot k

4. $\because$ $k,v_\perp$ 与 $w$ 两两垂直，且 $|w|=|v_\perp|$

   $\therefore$ 由向量积得
   \begin{aligned}
   w=k\times v_\perp&=k\times [v-(v\cdot k) k]\\
   &=k\times v-k\times (v\cdot k) k \\
   &= k\times v-k\times v_\parallel
   \end{aligned}
   \because k 与 v_\parallel 共线

   \therefore w=k \times v

5. $v_\perp$ 旋转 $\theta$ 角后得到 $v_{rot\perp}$

   将 $v_{rot\perp}$ 正交分解，得：$v_{rot\perp}=a+b$

   $a=v_{rot\perp}\times \cos(\theta-90^\circ)=v_{rot\perp}\times \cos,a=w\sin\theta$

   $b=v_{rot\perp}\times \cos(180^\circ-\theta)=v_{rot\perp}\times \cos,b=v_\perp\cos\theta$

   $\therefore v_{rot\perp}=a+b=w\sin\theta+v_{rot\perp}\cos\theta=\sin\theta k\times v + \cos \theta[v-(v\cdot k) k]$

6. 有\begin{aligned}
   v_{rot}=v_\parallel+v_{rot\perp}&=(v\cdot k)+\sin\theta k\times v+\cos\theta[v-(v\cdot k)k]\\
   &=(v\cdot k)k+\sin\theta k\times v + \cos\theta v-\cos\theta(v\cdot k)k\\
   &=\cos\theta v+(1-\cos\theta)(v\cdot k)k+\sin\theta k\times v
   \end{aligned}

7. 将得到的结果变为矩阵的形式：

   1. 推导，得：v_{rot}=\cos\theta v+(1-\cos\theta)(v\cdot k)k+\sin\theta k\times v

      把 k 和 v 分别写作列向量：
      k=\begin{pmatrix}
      k_x \\k_y \\k_z
      \end{pmatrix}
      v=\begin{pmatrix}
      v_x \\v_y \\v_z
      \end{pmatrix}
      令 v_{rot}=Rv，下面对 R 进行计算

   2. $(v\cdot k)k=k(v\cdot k)=k(k^T\cdot v)$

   3. $k\times v =\begin{pmatrix}k_y v_z-k_z v_y \\k_zv_x-k_xv_z \\k_xv_y-k_yv_x\end{pmatrix}=\begin{pmatrix}0&-k_z&k_y\\k_z&0&-k_x\\-k_y&k_x&0\end{pmatrix}\begin{pmatrix}v_x \\v_y \\v_z\end{pmatrix}$

   4. $\therefore\ R=I\cos\theta+(1-\cos\theta)\begin{pmatrix}k_x\\k_y \\k_z\end{pmatrix}\begin{pmatrix}k_x&k_y&k_z\end{pmatrix}+\sin\theta\begin{pmatrix}0&-k_z&k_y\\k_z&0&-k_x\\-k_y&k_x&0\end{pmatrix}$

      其中 $I$ 为 $3\times 3$ 的单位矩阵

如何将三维变成二维并在屏幕上显示出来

1. 模型变换 (M)
2. 相机变换 (V)
3. 投影变换 (P)

相机的定义

• 位置 \vec{e}
• 视线方向 \hat{g}
• 垂直方向 \hat{t}

如果把摄像机和世界一起变换，那么照片是一样的，所以把摄像机变换到新坐标系的原点，其他所有物体也做同样的变换

TEG 坐标系怎么转变为 XYZ 坐标系

M_{view}=R_{view}T_{view}

1. 先做平移，T_{view}=\begin{bmatrix} 1&0&0&-x_e\\ 0&1&0 &-y_e \\ 0& 0&1 &-z_e \\ 0&0&0 &1\end{bmatrix}

2. 再做旋转，顺着思路要把 \hat{g} 旋转到 -Z 坐标轴，把 \hat{t} 旋转到 Y 坐标轴，把 (g\times t) 旋转到 X 坐标轴，但这样的旋转矩阵非常难写

3. 所以采用逆向思路，把坐标轴移到相机坐标轴，通过逆操作写（该旋转矩阵为正交矩阵，其逆矩阵就是它的转置矩阵）（基变换）
   R^{-1}_{view}=\begin{bmatrix} x_{\hat{g}\times \hat{t}}&x_t&x_{-g}&0\\ y_{\hat{g}\times\hat{t}}&y_t&y_{-g} &0 \\ z_{\hat{g}\times\hat{t}}&z_t&z_{-g} &0 \\ 0&0&0 &1\end{bmatrix}\\
   R_{view}=\begin{bmatrix} x_{\hat{g}\times \hat{t}}&y_{\hat{g}\times\hat{t}}&z_{\hat{g}\times\hat{t}}&0\\ x_t&y_t&z_t &0 \\ x_{-g}&y_{-g}&z_{-g} &0 \\ 0&0&0 &1\end{bmatrix}\\

投影变换

计算机图形学中的投影

• 3D 转 2D
• 正交投影
• 透视投影

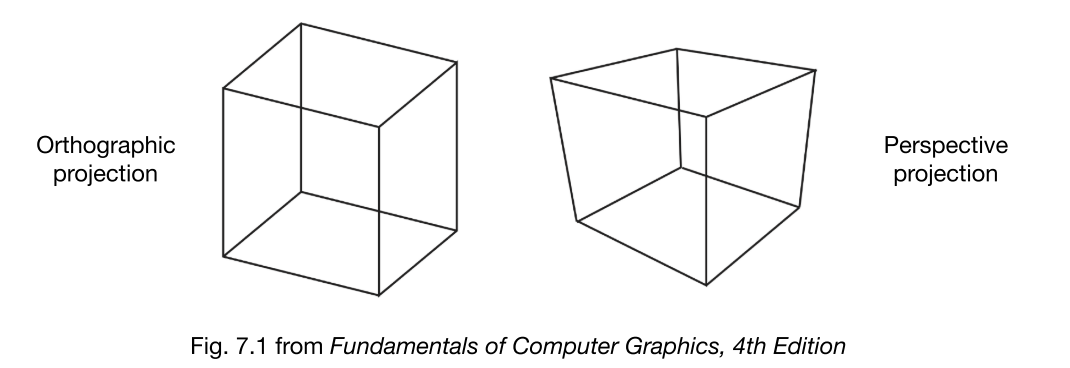
透视投影与正交投影

正交投影

• 相机位于原点，面向 -Z，上方是 Y
• 忽略 Z 坐标
• 将生成的矩形平移并缩放为 [-1, 1]^2

• 相机位置无限远，没有远近概念（忽略深度信息）

• 步骤：先做平移，再做缩放，目的是把投影全塞在 [-1,1]^3 的长方体内

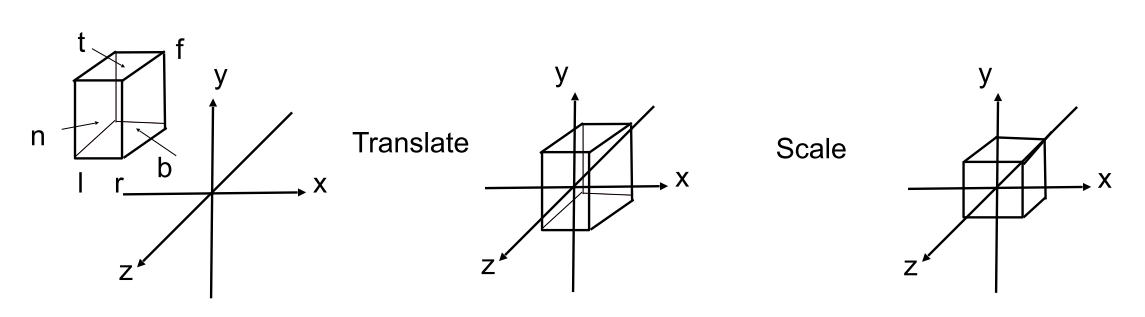
M_{ortho}=\begin{bmatrix} \dfrac{2}{r-l}&0&0&0\\ 0&\dfrac{2}{t-b}&0 &0 \\ 0&0&\dfrac{2}{n-f} &0 \\ 0&0&0 &1\end{bmatrix}\begin{bmatrix} 1&0&0&-\dfrac{r+l}{2}\\ 0&1&0 &=\dfrac{t+b}{2} \\ 0&0&1 &-\dfrac{n+f}{2} \\ 0&0&0 &1\end{bmatrix}

• 沿着 -Z 使远近不直观（n > f）
• 仅供参考：这就是 OpenGL 使用左手坐标的原因。

透视投影

• 最常见于计算机图形学、艺术、视觉系统
• 近大远小
• 平行线不平行； 收敛到单点

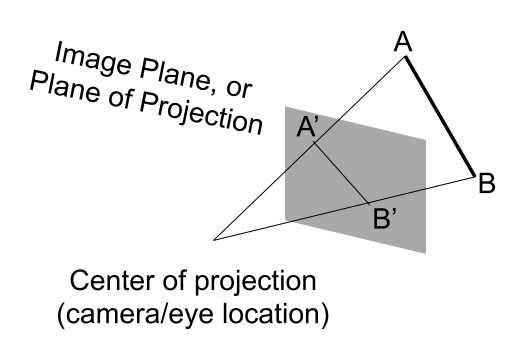
推导过程

正交投影矩阵的视锥体是一个四棱锥的一部分，其中近平面为 z=n，远平面为z=f，我们要把这个视锥体转换到一个正方体[-1,1][-1,1][-1,1] 中，可以先把远平面压缩，把视锥体压缩成一个长方体，然后再通过第二步中的正交投影矩阵就可以变换到正方体中，如图。

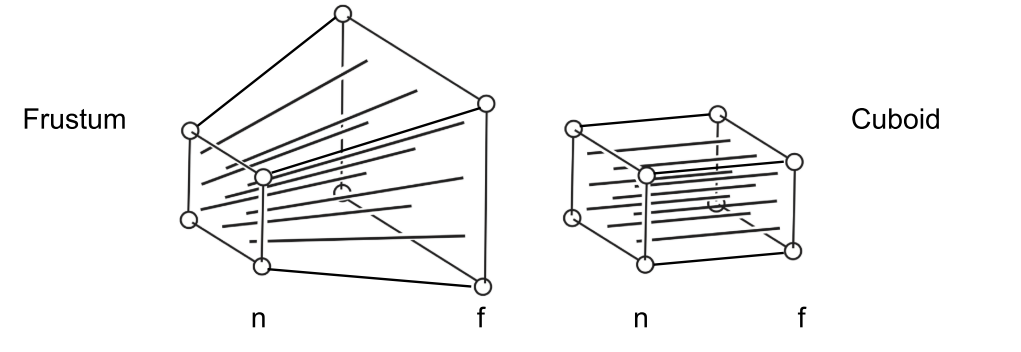
在把视锥体压缩成长方体的过程中，我们规定三个原则

1. 近平面的所有点坐标不变

2. 远平面的所有点坐标 z 值不变 都是 f

3. 远平面的中心点坐标值不变 为 (0,0,f)

然后我们假设视锥体内的任意一点 (x,y,z)，压缩以后的 xy 坐标应该与近平面上对应的点相同，如图解相似三角形可以得到 y\rightarrow ny/z,x\rightarrow nx/z

故对于(x,y,z,1)一点，它在视锥体压缩以后坐标应该为(nx/z,ny/z,unknow,1)。

z 值我们还不知道，这里先不讨论。
\begin{pmatrix}
x \\ y \\ z \\ 1
\end{pmatrix}\Rightarrow\begin{pmatrix}
nx/z \\ ny/z \\ \text{unknown} \\ 1
\end{pmatrix}
也就是我们现在需要找到一个矩阵 \text{Mpersp}\rightarrow\text{ortho}，使得上面的转换成立。

假设矩阵的第一行为 A,B,C,D。可以得到等式 Ax+By+Cz+D = nx/z。

然后我们发现这个等式好像很难求，如果让 A = n/z，其他等于0，的确可以得到结果。

但是矩阵的值应该是常数，n/z是个变量。

而其他的结果也很难写出来，同时矩阵的第二行也会有同样的问题 Ex+Fy+Gz+H = ny/z，也很难求。

所以我们换一种方法，前面根据已学知识可以知道(x,y,z,1)与(kx,ky,kz,k\not=0)这两个点是完全等价的点，

所以我们让k取z可以把坐标(nx/z,ny/z,unknow,1)变为(nx,ny,\text{still unknow},z)。
M_{presp\rightarrow ortho}^{(4\times 4)}\begin{pmatrix}
x \\ y \\ z \\ 1
\end{pmatrix}=\begin{pmatrix}
nx \\ ny \\ \text{unknown} \\ z
\end{pmatrix}
也就是我们需要找到矩阵 \text{Mpersp}\rightarrow\text{ortho}，使得上面的转换成立。

现在就变简单了，Ax+By+Cz+D = nx，求出 A=n,B=C=D=0

Ex+Fy+Gz+H = ny，求出 F=n,E=G=H=0

Mx+Ny+Oz+P = z，求出 O=1,M=N=P=0。
M_{presp\rightarrow ortho}\begin{pmatrix}
n&0&0&0 \\ 0&n&0&0 \\ ?&?&?&? \\ 0&0&1&0
\end{pmatrix}
于是，我们求出了矩阵的其中三行，只剩下第三行是未知的。

然后我们想下之前的三个原则，其中一个，近平面的所有点坐标不变。

也就是点 (x,y,n,1) 通过矩阵 \text{Mpersp}\rightarrow\text{ortho} 变换后，应该还是等于 (x,y,n,1)。
\begin{pmatrix}n &0&0 &0 \\0 &n&0&0\\? &? &? &? \\0 &0 &1 &0\end{pmatrix}*\begin{pmatrix}x\\y\\n\\1\end{pmatrix}=\begin{pmatrix}x\\y\\n\\1\end{pmatrix}
对于第一二四行，我们写出等式
nx+0y+0n+0_1=x\\
0x+ny+0n+0_1=y\\
0x+0y+1n+0*1=1\\
很明显这是有问题的，因为 n 应该是任意常数，但是现在只有在 n 等于 1 时，一二四行的运算才成立

所以我们根据前面的方法，再把 (x,y,n,1) 都乘以一个 n 等价变为 (nx,ny,n*n,n)。

这样转换就变成了
\begin{pmatrix}
n &0&0 &0 \\
0 &n&0&0\\
? &? &? &? \\
0 &0 &1 &0
\end{pmatrix}*\begin{pmatrix}
x\\y\\n\\1
\end{pmatrix}=\begin{pmatrix}
nx\\ny\\n*n\\n
\end{pmatrix}
对于第一二四行，我们写出等式
nx+0y+0n+0_1=nx\\
0x+ny+0n+0_1=ny\\
0x+0y+1n+0*1=n\\
完美成立。现在我们可以安心的求第三行了。

设第三行的四个数分别为 ABCD

可以获得等式 Ax+By+Cn+D = n*n。

明显 A=0,B=0,Cn+D = n*n ①

我们接下来考虑第三个原则，远平面的中心点坐标值不变 为(0,0,f)

同样为了保证之前求的矩阵一二四行成立，我们需要把 (0,0,f,1) 写成 (0,0,f*f,f)
\begin{pmatrix}
n &0&0 &0 \\
0 &n&0&0\\
? &? &? &? \\
0 &0 &1 &0
\end{pmatrix}*\begin{pmatrix}
0\\0\\f\\1
\end{pmatrix}=\begin{pmatrix}
0\\0\\f*f\\f
\end{pmatrix}

Cf+D = f*f ②

联立 ①②，解得：C = n+f,D = -nf

终于，我们求得了 \text{Mpersp}\rightarrow\text{ortho} 矩阵为

\begin{pmatrix}
n &0&0 &0 \\
0 &n&0&0\\
0 &0 &n+f &-nf \\
0 &0 &1 &0
\end{pmatrix}
也就是通过这个矩阵，我们可以把原来的透视投影的视锥体压缩为正交投影的视锥体（长方体）

最后我们再乘上一开始求出来正交投影矩阵 \text{Morth} 就得到了透视投影矩阵：\text{Mpersp} = \text{Mortho}*\text{Mpersp}\rightarrow\text{ortho}
\begin{pmatrix}2/(r-l)&0&0 &0 \\0 &2/(t-b)&0&0\\0 &0 &2/(n-f) &0 \\0 &0 &1 &1\end{pmatrix}*\begin{pmatrix}1&0&0 &-(l+r)/2 \\0 &1&0&-(b+t)/2\\0 &0 &1 &-(f+n)/2 \\0 &0 &0 &1\end{pmatrix}=\begin{pmatrix}n&0&0 &0 \\0 &n&0&0\\0 &0 &n+f &0 \\0 &0 &1 &0\end{pmatrix}